P13089 [FJCPC 2025] We are watching you!
题目背景
作弊哥是一个资深代打高手,他经常在 OCASU、oaiqnal、CPCX 等各种编程比赛中替别人代写代码,赚取了丰厚的收入。在比赛过程中,作弊哥会将题目的正确代码 $s_1$ 发送给作弊的参赛选手;这个参赛选手会在代码的 开头 随便加点没用的东西,构造出完整代码 $s$,就能提交。
作弊哥靠着这招屡试不爽。然而,这一次他不幸被官方盯上了。
作为官方的技术审查专家,小 A 需要对于选手提交的代码 $s$,分析 $s$ 的任意一个后缀的代码风格有多大概率出自于作弊哥。为了方便检验代码的同时,尽量不影响评测机速度,小 A 构造了一个能接受所有 $s$ 后缀的最小化确定型有限状态自动机(Deterministic Finite Automaton,DFA)。
接下来,小 A 按深度优先搜索的方法,遍历这个 DFA,并分析出状态 $i$ 和作弊哥的代码风格有 $c_i$ 点相似度。小 A 认为子串 $s'$ 的相似度为 DFA 在输出 $s'$ 的过程中,经过状态的最大相似度;而完整代码的相似度为其所有非空子串相似度的平均值。
现在,小 A 拿到了一些选手的完整代码 $s$,依此构建了最小化 DFA,并按深度优先搜索的遍历方法给出了 DFA 各状态的相似度。请你帮忙评估这些代码和作弊哥代码的相似度。
如果你不了解 DFA 以及 DFA 的深度优先遍历,请阅读补充提示。
题目描述
形式化的,以下代码描述了上述过程以及需求,但由于过大的时间复杂度,需要你优化并使其可以通过本题。
```cpp
#include
using i64 = long long;
struct SAM {
struct Node {
int fa, len;
std::array trans;
Node() : fa{}, len{}, trans{} {}
};
std::vector t;
SAM() : t(2) {}
int New() {
t.push_back(Node());
return t.size() - 1;
}
int extend(int lst, int c) {
int u = lst, v;
if (trans(u, c)) {
if (len(u) + 1 == len(v = trans(u, c))) {
return v;
}
int x = New();
len(x) = len(u) + 1, fa(x) = fa(v);
t[x].trans = t[v].trans;
for (fa(v) = x; u && trans(u, c) == v; trans(u, c) = x, u = fa(u));
return x;
}
int x = New();
len(x) = len(u) + 1;
for(; u && !trans(u, c); trans(u, c) = x, u = fa(u));
if (!u) {
fa(x) = 1;
} else if (len(u) + 1 == len(v = trans(u, c))) {
fa(x) = v;
} else {
int w = New();
len(w) = len(u) + 1, fa(w) = fa(v);
t[w].trans = t[v].trans;
for (fa(v) = fa(x) = w; u && trans(u, c) == v; trans(u, c) = w, u = fa(u));
}
return x;
}
int& fa(int x) { return t[x].fa; }
int& len(int x) { return t[x].len; }
int& trans(int x, int c) { return t[x].trans[c]; }
};
void solve() {
std::string s;
std::cin >> s;
SAM sam;
int lst = 1;
for (auto c : s) { // 请注意这里是建立后缀自动机
lst = sam.extend(lst, c - 'a');
}
std::vector c(sam.t.size());
for (int i = 1; i < c.size(); i++) {
std::cin >> c[i];
}
i64 ans = 0;
for (int i = 0; i < s.size(); i++) {
int now = c[1], x = 1;
for (int j = i; j >= 0; j--) {
x = sam.trans(x, s[j] - 'a');
now = std::max(now, c[x]);
ans += now;
}
}
std::cout T;
while (T--) {
solve();
}
return 0;
}
```
输入格式
本题包含多组测试数据。
第一行是一个正整数 $T$($1\leq T\leq 2\times 10^5$),表示有 $T$ 份完整代码。
接下来 $T$ 组数据。第一行是一个由小写字母组成的字符串 $S$,表示选手提交的代码。保证字符串长度 $|S|$ 满足($1\leq |S|\leq 2\times 10^5$)。
第二行由 $m$ 个整数 $c_1, c_2, \cdots, c_m$($1\leq c_i\leq 2\times 10^5$)构成。其中 $m$ 表示小 A 构造的最小化 DFA 的状态数,$c_i$ 表示这个 DFA 按深度优先搜索,访问到的第 $i$ 个状态的相似度。
数据保证 $\sum|S|\leq 2\times 10^5$;数据保证对于每组的字符串 $S$,其所有后缀构成的最小化 DFA 状态数恰好为 $m$。
输出格式
输出包含 $T$ 行,其中第 $i$ 行表示第 $i$ 份代码的相似度。
为了避免除法运算,对于每个提问 $S$,你只需要输出答案乘上 $\frac{|S|\cdot (|S|+1)}{2}$,答案可以保证这是个整数。
说明/提示
1. 确定型有限状态自动机(DFA)
确定型有限状态自动机(DFA)是一个状态机。它从固定的起始状态 $q_0$ 出发,不断读入字符 $c$,并不断依此跳到后续状态;读入不同的字符将会跳转到不同的后续状态。如果读入完整个字符串后停在"接受状态",我们认为 DFA 接受这个字符串;否则,认为 DFA 不接受这个字符串。特别的,如果 DFA 在某个状态 $q$ 时读入字符 $c$ 无后续状态,我们同样认为 DFA 不接受这个字符串。
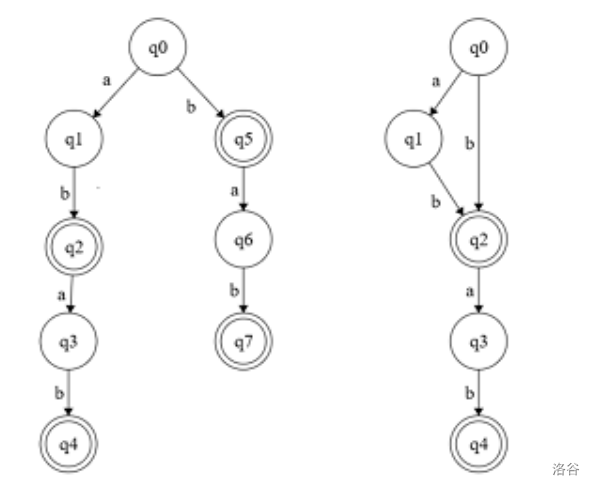
如下图所示,带两个圆的状态为接受状态。左侧的 DFA 从初始状态 $q_0$ 开始,读入 abab、bab、ab、b 后会分别停止于 $q_4, q_7, q_2, q_5$,均是接受状态;且读入其他字符串均不能进入接受状态。因此左侧的 DFA 可以接受 abab 的所有后缀;右侧的同理。
对于能识别相同字符串的所有 DFA,我们认为状态最少的 DFA 就是最小化 DFA。可以证明,不同的最小化 DFA 可以通过给状态重新编号,而变成相同的 DFA。
如该图所示,左右两侧的 DFA 均只能接受 abab、bab、ab、b 这四个字符串,因此两者等价。此外,可以证明,右侧的 DFA 是能识别这类字符串的最小化 DFA。
2. DFA 的深度优先遍历
DFA 的深度优先遍历将从起始状态 $q_0$ 开始,每次选择当前状态未访问的、按字母表从小到大的下一个字符对应的边,直到遍历完所有状态。各状态的编号即为其被访问到的顺序。
如左侧的 DFA 的深度优先遍历顺序为 $q_0, q_1, q_2, q_3, q_4, q_5, q_6, q_7$;
右侧 DFA 的深度优先遍历顺序为 $q_0, q_1, q_2, q_3, q_4$。