P13092 [FJCPC 2025] 二叉树

墨菲特非常喜欢完美的树。在某一天，他决定用茂凯给的神秘种子自己种一棵树。 这颗种子拥有非常旺盛的生命力。将这颗种子种下后，如果我们把第一天种下的种子记为初始的叶子节点，那么从第二天开始，每个前一天长出来的叶子节点，都会长出两个新的叶子节点。换句话说，如果这颗树生长了 $k$ 天，那么它就是一棵拥有 $2^k - 1$ 个节点的满二叉树。 由于其迅速的生长速度，墨菲特很快就能得到一棵拥有很多节点的满二叉树，他认为满二叉树是十分完美的。 茂凯也知道墨菲特非常喜欢树，因此他带来了一份礼物：由同样的神秘种子种出来的一棵树（大小不一定相同）。然而墨菲特已经有一颗这样的树了，两棵树的存放不太方便，于是他在两棵树之间连接了一条新的边，这样就是一棵树了。 显然，这样的树已经不是完美的二叉树了，因此墨菲特很快就把他丢在了角落。 过了很久很久之后，墨菲特又想起来了这棵由两棵满二叉树连接形成的新树，他想要重新把这棵树拆成两棵满二叉树，但是他已经忘记哪条边是他额外添加上去的了。 希望聪明的你可以帮助墨菲特解决这个问题。 形式化地，给定一棵树，你需要删除其中的一条边，使得分成的两棵树都是满二叉树，保证至少存在一个解。 *所有叶结点的深度均相同，且所有非叶节点的子节点数量均为 $2$ 的二叉树称为满二叉树。

**输入包含多组测试数据。** 第一行包含一个正整数 $T$ ( $1 \le T \le 10^5$ ) ，表示测试数据的数量。接下来是测试数据的描述。 每组测试数据的第一行包含一个正整数 $n\ (2 \le n \le 2^{17} - 2)$ ，表示墨菲特手上的树的节点个数。 接下来 $n - 1$ 行，每行两个由空格分开的正整数 $u_i, v_i\ (1 \le u_i, v_i \le n)$ ，表示树上的一条边 $(u_i, v_i)$ 。输入保证给定的边集构成一棵树。 另外，保证 $\sum n \le 10^6$ 。

对于每一组测试数据，输出一行一个正整数 $i$ ，表示如果删除了给定边集中的第 $i$ 条边 $(u_i, v_i)$ ，分成的两棵树都是满二叉树。保证这样的解一定存在。如果有多个可行的解，输出任意一个即可。

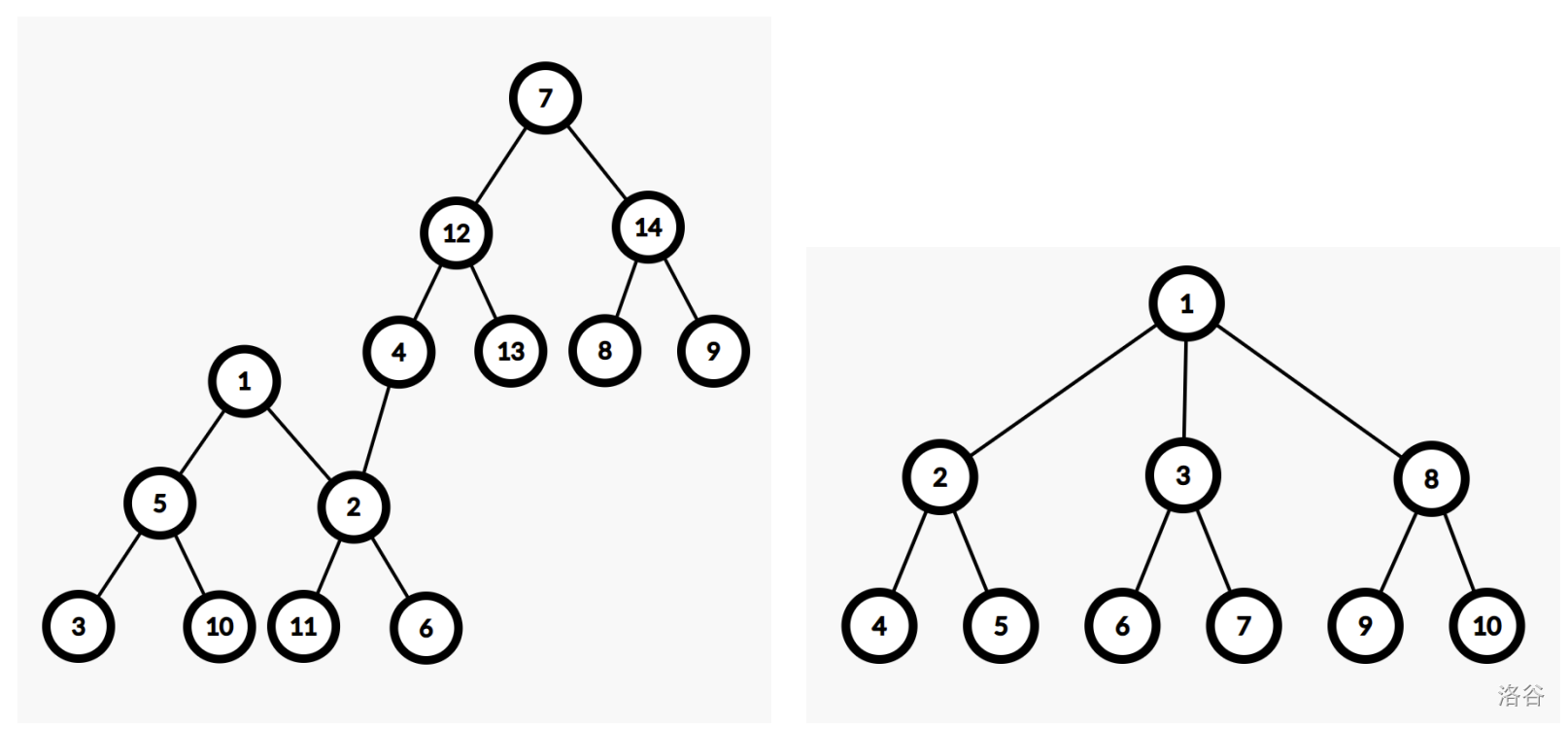
 第二组样例的树如上图所示，可以发现，只有删除边 $(2, 4)$ 是合法的。 第三组样例的树如下图所示，可以发现，删除边 $(1, 2), (1, 3), (1, 8)$ 都是合法的，你可以输出任意一种。