P1309 [NOIP 2011 Junior] Swiss-system Tournament

In head-to-head competitive sports such as table tennis, badminton, and chess, the most common formats are knockout and round-robin. The former requires fewer matches and each match is tense and exciting, but it is more random. The latter is fairer and less random, but the process is often very long. The Swiss-system format introduced in this problem is named after its earliest use in an international chess tournament held in Switzerland in 1895. It can be seen as a compromise between knockout and round-robin: it ensures stability while keeping the schedule from becoming too long.

$2 \times N$ players, numbered $1 \sim 2 \times N$, play $R$ rounds. Before each round starts, and after all matches are finished, players are ranked in descending order by total points. A player's total points equal the initial points before round $1$ plus the sum of points earned in all matches already played. If the total points are the same, the player with the smaller id ranks ahead. The pairings of each round depend on the ranking at the start of that round: rank $1$ vs rank $2$, rank $3$ vs rank $4$, ..., rank $2 \times K - 1$ vs rank $2 \times K$, ..., rank $2 \times N - 1$ vs rank $2 \times N$. The winner of each match gets $1$ point and the loser gets $0$ points. That is, except for the first round, the arrangements of the other rounds cannot be determined in advance; they depend on the players' performances in previous matches. Given each player's initial points and strength value, compute the id of the player ranked $Q$-th after $R$ rounds. We assume all strength values are pairwise distinct, and in every match the player with the higher strength always wins.

The first line contains three positive integers $N, R, Q$, separated by single spaces, indicating there are $2 \times N$ players, $R$ rounds, and we are interested in the $Q$-th place. The second line contains $2 \times N$ non-negative integers $s_1, s_2, \dots, s_{2 \times N}$, separated by single spaces, where $s_i$ denotes the initial points of the player with id $i$. The third line contains $2 \times N$ positive integers $w_1, w_2, \dots, w_{2 \times N}$, separated by single spaces, where $w_i$ denotes the strength value of the player with id $i$.

Output a single integer: the id of the player ranked $Q$-th after $R$ rounds.

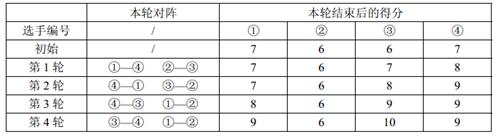
Sample Explanation:  Constraints: - For $30\%$ of the testdata, $1 \le N \le 100$. - For $50\%$ of the testdata, $1 \le N \le 10000$. - For $100\%$ of the testdata, $1 \le N \le 10^5$, $1 \le R \le 50$, $1 \le Q \le 2 \times N$, $0 \le s_1, s_2, \dots, s_{2 \times N} \le 10^8$, $1 \le w_1, w_2, \dots, w_{2 \times N} \le 10^8$. NOIP 2011 Junior Problem 3. Translated by ChatGPT 5