P13151 [GCJ 2018 #3] Raise the Roof

人类学家们对某个古希腊几何学家社团有了令人惊讶的发现：他们对聚会的热爱丝毫不亚于对数学的热爱！事实上，随着年复一年的聚会规模不断扩大，他们不得不不断抬高舞厅的屋顶，以保持噪音在可接受的水平。 我们知道，他们舞厅的屋顶始终由恰好三根柱子的顶端支撑；这些柱子是从地板上垂直升起的无限细线段。每当社团想要抬高屋顶时，他们会先拆除现有的屋顶。然后，在一个还没有柱子的地方建造一根新柱子。最后，用新柱子和之前建造的柱子中最近的两根柱子的顶端作为支点，搭建新的屋顶。出于神秘的原因，任意三根柱子的底座都不会共线，任意四根柱子的顶端也不会共面。 每一块屋顶都是一个凸多边形，属于由三根支撑柱顶端确定的平面。对于每一根在支撑柱之前建造的柱子，屋顶不会与该柱子有任何交点，并且屋顶足够大，可以覆盖该柱子顶端的上方空间。屋顶不会接触地板。不同的屋顶形状不一定完全相同。 在一次考古发掘中，你找到了社团曾经建造过的所有 $N$ 根柱子，但没有发现任何屋顶。你想要确定一种可能的柱子建造顺序，使其符合上述规则。一个可能的顺序是对 $N$ 根柱子的一个排列，使得对于该排列的每一个长度不少于 4 的前缀，存在一块屋顶（凸多边形），它包含该前缀最后三根柱子的顶端，并且对于前缀中的其它每一根柱子，若其顶端为 $(x, y, h)$，则屋顶上存在一个点 $(x, y, z)$ 满足 $z > h$。

输入的第一行包含测试用例数 $T$。接下来有 $T$ 组测试数据。每组测试数据的第一行包含一个整数 $N$，表示柱子的数量。接下来的 $N$ 行，每行包含三个整数 $X_i$、$Y_i$ 和 $H_i$，分别表示第 $i$ 根柱子顶端的 $X$ 坐标、$Y$ 坐标和离地高度。

对于每组测试数据，输出一行，格式为 `Case #x: y1 y2 ... yN`，其中 $x$ 是测试用例编号（从 1 开始），$y_i$ 是 $1$ 到 $N$ 之间的不同整数，表示第 $i$ 根被建造的柱子在输入中的编号。 保证至少存在一种合法答案。如果有多种可能的答案，你可以输出其中任意一种。

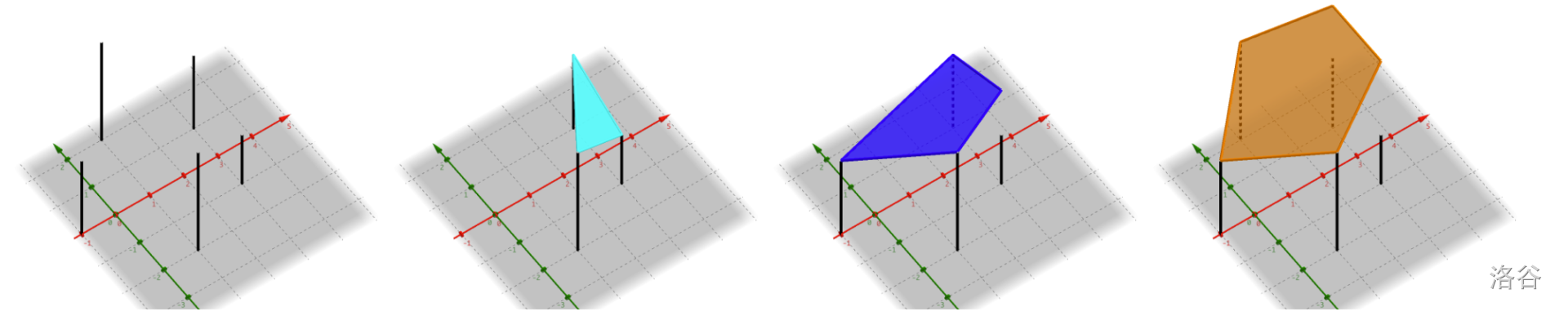
**样例解释** 下图展示了样例第 1 组数据的情况。  **数据范围** - $1 \leq T \leq 100$。 - $-10^6 \leq X_i \leq 10^6$，对所有 $i$。 - $-10^6 \leq Y_i \leq 10^6$，对所有 $i$。 - $1 \leq H_i \leq 10^6$，对所有 $i$。 - 任意不同的 $i, j, k$，$(X_i, Y_i)$、$(X_j, Y_j)$ 和 $(X_k, Y_k)$ 不共线。 - 任意不同的 $i, j, k, l$，$(X_i, Y_i, H_i)$、$(X_j, Y_j, H_j)$、$(X_k, Y_k, H_k)$ 和 $(X_l, Y_l, H_l)$ 不共面。 **测试点 1（7 分，公开）** - $4 \leq N \leq 10$。 **测试点 2（19 分，隐藏）** - $4 \leq N \leq 1000$。 由 ChatGPT 4.1 翻译