P13196 [GCJ 2016 #1C] Slides!

Gooli 是一家在丘陵地区拥有 $\mathbf{B}$ 座大楼的巨型公司。这些大楼编号为 $1$ 到 $\mathbf{B}$。 CEO 希望在大楼之间建设一组滑梯，方便她从自己在 1 号大楼的办公室前往她最喜欢的咖啡馆所在的 $\mathbf{B}$ 号大楼。滑梯当然是单向的，但由于大楼都很高且有电梯，滑梯可以从任意一栋大楼出发，通向任意另一栋大楼，方向不限。具体来说，对于任意两栋大楼 $\mathrm{x}$ 和 $\mathrm{y}$，你可以选择建造 $0$ 条或 $1$ 条从 $\mathrm{x}$ 到 $\mathrm{y}$ 的滑梯，也可以选择建造 $0$ 条或 $1$ 条从 $\mathrm{y}$ 到 $\mathrm{x}$ 的滑梯。唯一的例外是，不允许从 $\mathbf{B}$ 号大楼出发建滑梯，因为 CEO 一旦到达那里，就不再需要继续滑行。 为了纪念 Gooli 公司成立恰好 $\mathbf{M}$ 毫秒，设计方案必须确保 CEO 恰好有 $\mathbf{M}$ 种不同的方式从 1 号大楼滑到 $\mathbf{B}$ 号大楼。一种方式定义为一个以 1 号大楼为起点、以 $\mathbf{B}$ 号大楼为终点的楼栋序列，且序列中任意相邻的两栋楼之间都存在一条滑梯。注意，CEO 并不要求任意两栋大楼之间都能通过滑梯互达。 你能否给出一种包含一条或多条滑梯的方案，使得 CEO 的要求得到满足？或者判断这种方案是否不可能存在？

输入的第一行包含一个整数 $\mathbf{T}$，表示测试用例数量。接下来有 $\mathbf{T}$ 行，每行包含两个整数 $\mathbf{B}$ 和 $\mathbf{M}$，含义如上所述。

对于每组测试用例，输出一行 `Case #x: y`，其中 $\mathrm{x}$ 是测试用例编号（从 1 开始），$\mathrm{y}$ 是单词 POSSIBLE 或 IMPOSSIBLE，表示能否满足 CEO 的要求。如果可行，接下来输出 $\mathbf{B}$ 行，每行包含 $\mathbf{B}$ 个字符，描述一个合法的滑梯建设方案。第 $\mathrm{i}$ 行第 $\mathrm{j}$ 个字符为 1 表示应从第 $\mathrm{i}$ 栋大楼到第 $\mathrm{j}$ 栋大楼建一条滑梯，否则为 0。第 $\mathrm{i}$ 行第 $\mathrm{i}$ 个字符始终为 0，最后一行的所有字符也应全为 0。 如果存在多种合法方案，你可以输出任意一种。

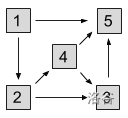
**样例解释** 样例输出展示了每组数据的一种可行方案，其他方案也是可能的。 以下是第 1 组样例方案的示意图：  从 1 号大楼到 5 号大楼共有 4 种方式： - 1 → 5 - 1 → 2 → 3 → 5 - 1 → 2 → 4 → 5 - 1 → 2 → 4 → 3 → 5 在第 3 组中，如果建造 1→2、2→3、3→1、1→4 的滑梯，则 CEO 可以有无数种方式到达 4 号大楼（可以直接到 4，也可以绕环多次后再到 4），但 CEO 要求恰好 20 种方式。 **限制条件** $1 \leqslant \mathbf{T} \leqslant 100$。 **小数据集（13 分，测试集 1 - 可见）** - $2 \leqslant \mathbf{B} \leqslant 6$。 - $1 \leqslant \mathbf{M} \leqslant 20$。 **大数据集（21 分，测试集 2 - 隐藏）** - $2 \leqslant \mathbf{B} \leqslant 50$。 - $1 \leqslant \mathbf{M} \leqslant 10^{18}$。 翻译由 GPT4.1 完成。