P13210 [GCJ 2016 Finals] Radioactive Islands

你正驾驶一艘船，从坐标 $(-10, A)$ 出发，前往坐标 $(10, B)$。所有坐标单位均为千米，且你的船以恒定速度 1 千米/小时行驶。你可以完全自主规划航线。我们将船视为一个点。 该区域内有 $\mathbf{N}$ 座岛屿；每座岛屿也被视为一个点。第 $i$ 座岛屿位于 $(0, \mathbf{C}_i)$。 该区域存在放射性，无论你身处何处，每小时都会受到 1 微西弗的环境辐射。此外，每座岛屿本身也具有放射性，你每小时还会从第 $i$ 座岛屿额外受到 $(\mathbf{D}_i)^{-2}$ 微西弗的辐射，其中 $\mathbf{D}_i$ 是你当前与第 $i$ 座岛屿的距离（单位：千米）。（形式化地说：设 $\mathbf{D}_i(\mathbf{t})$ 为你在时刻 $\mathbf{t}$ 与第 $i$ 座岛屿的距离，$\mathbf{X}$ 为你完成旅程所需的总时间。那么你从第 $i$ 座岛屿获得的总辐射量为 $\int_0^\mathbf{X} \mathbf{D}_i(\mathbf{t})^{-2} d\mathbf{t}$。）你可以任意接近某个岛屿，只要不与其精确重合。 请问，如果你最优规划航线，你能收到的最小总辐射剂量是多少？

输入的第一行包含一个整数 $\mathbf{T}$，表示测试用例数。接下来有 $\mathbf{T}$ 组测试用例，每组包含两行。每组的第一行包含三个值：一个整数 $\mathbf{N}$，以及两个浮点数 $\mathbf{A}$ 和 $\mathbf{B}$，意义如上文所述。第二行包含 $\mathbf{N}$ 个浮点数 $\mathbf{C}_i$，第 $i$ 个数表示第 $i$ 座岛屿的纵坐标。 所有浮点数精确到小数点后两位。

对于每组测试用例，输出一行 `Case #x: y`，其中 $\mathbf{x}$ 为测试用例编号（从 1 开始），$\mathbf{y}$ 为你在完成航行过程中能收到的最小总辐射剂量（单位：微西弗）。 如果 $\mathbf{y}$ 与正确答案的绝对误差或相对误差不超过 $10^{-3}$，则视为正确。

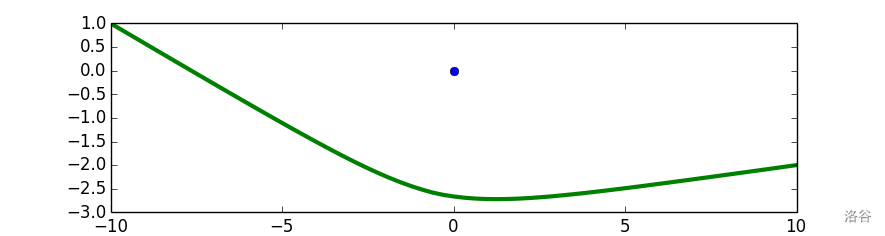
**样例解释** 下图展示了样例第 1 组的最优路径。我们已将岛屿放大以便观察，但在计算时应视为一个点。  **限制条件** - $-10.00 \leq \mathbf{A} \leq 10.00$。 - $-10.00 \leq \mathbf{B} \leq 10.00$。 - 对所有 $i$，$-10.00 \leq \mathbf{C}_i \leq 10.00$。 - 对所有 $i \neq j$，$\mathbf{C}_i \neq \mathbf{C}_j$。 **小数据集（25 分，测试集 1 - 可见）** - 时间限制：~~120~~ 30 秒。 - $\mathbf{T} \leq 20$； - $\mathbf{N} = 1$。 **大数据集（25 分，测试集 2 - 隐藏）** - 时间限制：~~240~~ 60 秒。 - $\mathbf{T} \leq 50$； - $1 \leq \mathbf{N} \leq 2$。 翻译由 GPT4.1 完成。