P13214 [GCJ 2015 Qualification] Ominous Omino

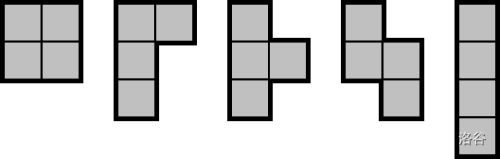
一个 $N$-omino 是由 $N$ 个单位方格通过边完全连接而成的二维图形。更正式地说，$1$-omino 是一个 $1\times 1$ 的单位正方形，而 $N$-omino 是在一个 $(N-1)$-omino 的某一条或多条边上连接一个相邻的 $1\times 1$ 单位正方形。对于本题，如果两个 $N$-omino 通过旋转和/或翻转可以互相变换，则认为它们是相同的。例如，下面是所有可能的五种 $4$-omino：  下面是 $108$ 种可能的 $7$-omino 中的一部分：  Richard 和 Gabriel 要玩一个游戏，规则如下，给定预先确定的 $\mathbf{X}$、$\mathbf{R}$ 和 $\mathbf{C}$： 1. Richard 可以选择任意一种可能的 $\mathbf{X}$-omino。 2. Gabriel 必须至少使用一个该 $\mathbf{X}$-omino，并可以任意多次使用任意 $\mathbf{X}$-omino（包括 Richard 选择的那一个），将 $\mathbf{R}\times\mathbf{C}$ 的网格完全填满，不能有重叠或溢出。也就是说，每个格子必须被恰好一个 $\mathbf{X}$-omino 的单元格覆盖，且不能有 $\mathbf{X}$-omino 超出网格范围。Gabriel 可以随意旋转或翻转任意数量的 $\mathbf{X}$-omino，包括 Richard 选择的那一个。如果 Gabriel 能完全填满网格，则他获胜；否则，Richard 获胜。 给定特定的 $\mathbf{X}$、$\mathbf{R}$ 和 $\mathbf{C}$，Richard 能否选择一种 $\mathbf{X}$-omino 保证自己获胜，还是无论 Richard 选择什么，Gabriel 都必胜？

输入的第一行包含测试用例数 $\mathbf{T}$。接下来的 $\mathbf{T}$ 行，每行包含三个用空格分隔的整数：$\mathbf{X}$、$\mathbf{R}$ 和 $\mathbf{C}$。

对于每个测试用例，输出一行，格式为 `Case #x: y`，其中 $x$ 是测试用例编号（从 1 开始），$y$ 为 `RICHARD`（如果存在至少一种选择能保证 Richard 获胜）或 `GABRIEL`（如果无论 Richard 选择什么 Gabriel 都能获胜）。

**样例解释** 对于第 1 个样例，Richard 只有一种 $2$-omino 可选——由两个单位格组成的 $1\times 2$ 长条。不论 Gabriel 如何放置这个长条，都可以用另一个 $1\times 2$ 长条正好填满 $2\times 2$ 的网格，所以 Gabriel 获胜。 对于第 2 个样例，Richard 只能选择 $1\times 2$ 的长条，但无论 Gabriel 如何放置它，都会剩下一个 $1\times 1$ 的空格，无法用 $2$-omino 填满，所以 Richard 获胜。 对于第 3 个样例，Richard 可以选择 $2\times 2$ 的正方形 $4$-omino。这个正方形无法完整放入 $4\times 1$ 的网格，因此 Richard 获胜。 对于第 4 个样例，Richard 可以选择直线型 $3$-omino 或 L 形 $3$-omino。无论选择哪种，Gabriel 都可以用它填满网格。 **数据范围** **小数据集（8 分）** - 时间限制：5 秒。 - $\mathbf{T} = 64$。 - $1 \leq \mathbf{X}, \mathbf{R}, \mathbf{C} \leq 4$。 **大数据集（26 分）** - 时间限制：10 秒。 - $1 \leq \mathbf{T} \leq 100$。 - $1 \leq \mathbf{X}, \mathbf{R}, \mathbf{C} \leq 20$。 由 ChatGPT 4.1 翻译