P13227 [GCJ 2015 #2] Drum Decorator

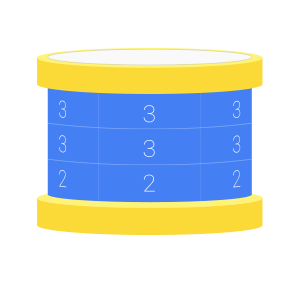
你是摇滚乐队 Denise and the Integers 的鼓手。你的鼓是一个圆柱体，你在鼓面上包裹了一张矩形网格。 你的乐队即将在 Mathland 演出。Mathland 的观众非常挑剔，他们要求你的鼓面上的每个格子都填上正整数，不能有零或负数。此外，每个整数 $K$ 必须恰好与 $K$ 个相同整数的格子相邻（即共享一条边，而不仅仅是一个点）。也就是说，一个填了 $1$ 的格子，必须恰好与一个填了 $1$ 的格子相邻；一个填了 $2$ 的格子，必须恰好与两个填了 $2$ 的格子相邻，依此类推。除此之外，格子与其它格子的接触情况没有限制。（鼓的顶部和底部不是格子，不需要装饰。注意，这意味着鼓面最上面和最下面一行的格子每个只与三个格子相邻，而其它格子每个与四个格子相邻。） 例如，下图是一个 $3$ 行 $5$ 列的圆柱鼓面的一种合法装饰方式：  （请想象鼓背面的两列与正面看到的三列是连续相连的。） 你想知道有多少种不同的合法装饰方案。如果两个装饰无法通过绕圆柱轴旋转得到彼此，则认为它们是不同的。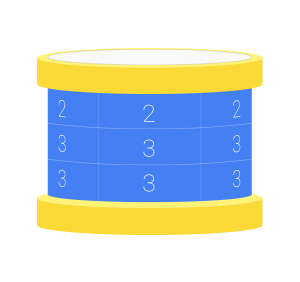鼓的顶部和底部视为不同，因此下图的 $3\times 5$ 鼓面装饰与上图不同：  （同样，鼓背面的两列与正面三列是连续相连的。） 你的鼓有 $\mathbf{R}$ 行和 $\mathbf{C}$ 列。请问有多少种不同的合法装饰方案？答案可能很大，请输出方案数对 $10^9+7$（$1000000007$）取模后的结果。

第一行输入测试用例数 $\mathbf{T}$。接下来的 $\mathbf{T}$ 行，每行包含两个用空格分隔的整数 $\mathbf{R}$ 和 $\mathbf{C}$，分别表示鼓面的行数和列数。

对于每个测试用例，输出一行，格式为 "Case #$x$: $y$"，其中 $x$ 是测试用例编号（从 1 开始），$y$ 是合法装饰方案数对 $10^9+7$ 取模后的结果。

**样例解释** 对于第 1 个样例，唯一的方案是所有格子都填 $3$。 对于第 2 个样例，只有题目描述中给出的两种方案。 **小数据集（11 分）** - 时间限制：5 秒。 - $1 \leq \mathrm{T} \leq 20$。 - $2 \leq \mathrm{R} \leq 6$。 - $3 \leq \mathrm{C} \leq 6$。 **大数据集（10 分）** - 时间限制：10 秒。 - $1 \leq \mathrm{T} \leq 100$。 - $2 \leq \mathrm{R} \leq 100$。 - $3 \leq \mathrm{C} \leq 100$。 由 ChatGPT 4.1 翻译