P13241 「2.48sOI R1」格律树

平平仄仄平平仄，仄仄平平仄仄平。

来自 CodeForces 的 Che960 想学习如何作近体诗。为此，他咨询了来自洛谷的 lizihan250。lizihan250 告诉他，诗句中的每个字都可以根据发音分为“平声”或“仄声”。除首句外，每一联的上句必须以“平声”收尾，下句必须以“仄声”收尾。每一句内应避免“孤平”。本题中，我们认为，若一句诗句中存在连续的三个字依次为“仄声”、“平声”、“仄声”，我们就认为，这句诗句出现了“孤平”。本题不考虑对仗、押韵等其他要求。 Che960 为了练习平仄的运用，构造了一棵以 $1$ 号节点为根的格律树，树上的每个节点都代表“平声”或“仄声”中的一种。Che960 会进行多次练习，每次练习时，Che960 会在树上选出一些“关键点”，并指定了这些“关键点”代表的是“平声”还是“仄声”。Che960 的任务就是给定一种方案，给树上所有非关键节点指定其代表的是“平声”还是“仄声”，使得从根节点到任意一个“关键点”的简单路径上的所有节点依次排列成的诗句不出现“孤平”。 lizihan250 看到了这个练习之后，想到了这样一个问题：对于 Che960 的每次练习，他最多能给出多少种不同的方案？两种方案不同，当且仅当存在至少一个节点，在两种方案中分别被指定为“平声”与“仄声”。答案对 $10^9+7$ 取模。 ### 形式化题意 我们用 $0$ 指代上文的“平声”，用 $1$ 指代上文的“仄声”。 给定一棵树，每个节点有 $01$ 点权。进行多次询问，每次询问选择若干个节点，指定它们的点权。求：若剩下的点的点权可以任意指定，则有多少种指定点权的方法，使得任意一个指定点到根节点的路径上，不存在连续的三个节点的点权依次为 $1$，$0$ 和 $1$。

第一行，一个正整数 $n$，表示树的节点总数。 接下来 $n-1$ 行，每行两个正整数 $u,v$，表示树上编号为 $u,v$ 的两点之间连有一条边。 接下来两个正整数 $t,q$，分别表示 Che960 的练习次数与输出参数。输出参数的作用会在“输出格式”部分给出。 接下来 $t$ 组数据，第 $i$ 组数据中，第一行一个正整数 $k_i$，表示这轮联系中共有 $k_i$ 个“关键点”。接下来 $k_i$ 行，第 $j$ 行两个正整数 $p_{i,j},s_{i,j}$，表示编号为 $p_{i,j}$ 的节点被指定为 $s_{i,j}$。其中，若 $s_{i,j}=0$，则该节点被指定为“平声”，否则，该节点被指定为“仄声”。

共 $\left\lfloor\dfrac{t}{q}\right\rfloor$ 行，每行一个整数，第 $i$ 行表示 Che960 第 $(i-1) \times q + 1$ 次至第 $i \times q$ 次练习的方案数对 $10^9+7$ 取模的异或和的值。

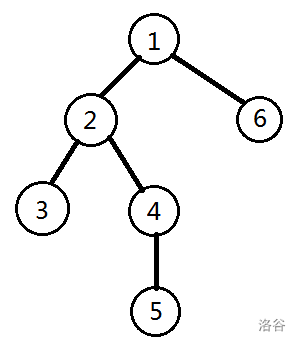
### 样例解释 对于样例一，样例中呈现的树的形态如下图所示：  第一次练习选取 $3$ 号节点、$6$ 号节点作为“关键点”，分别指定为“仄声”，“平声”。共 $12$ 种方案，如下表所示（标红的为“关键点”的声调）： | 方案编号 | $1$ 号节点 | $2$ 号节点 | $3$ 号节点 | $4$ 号节点 | $5$ 号节点 | $6$ 号节点 | | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | | $1$ | 平 | 平 | $\color{red}\text{仄}$ | 平 | 平 | $\color{red}\text{平}$ | | $2$ | 平 | 平 | $\color{red}\text{仄}$ | 平 | 仄 | $\color{red}\text{平}$ | | $3$ | 平 | 平 | $\color{red}\text{仄}$ | 仄 | 平 | $\color{red}\text{平}$ | | $4$ | 平 | 平 | $\color{red}\text{仄}$ | 仄 | 仄 | $\color{red}\text{平}$ | | $5$ | 平 | 仄 | $\color{red}\text{仄}$ | 平 | 平 | $\color{red}\text{平}$ | | $6$ | 平 | 仄 | $\color{red}\text{仄}$ | 平 | 仄 | $\color{red}\text{平}$ | | $7$ | 平 | 仄 | $\color{red}\text{仄}$ | 仄 | 平 | $\color{red}\text{平}$ | | $8$ | 平 | 仄 | $\color{red}\text{仄}$ | 仄 | 仄 | $\color{red}\text{平}$ | | $9$ | 仄 | 仄 | $\color{red}\text{仄}$ | 平 | 平 | $\color{red}\text{平}$ | | $10$ | 仄 | 仄 | $\color{red}\text{仄}$ | 平 | 仄 | $\color{red}\text{平}$ | | $11$ | 仄 | 仄 | $\color{red}\text{仄}$ | 仄 | 平 | $\color{red}\text{平}$ | | $12$ | 仄 | 仄 | $\color{red}\text{仄}$ | 仄 | 仄 | $\color{red}\text{平}$ | 所有指定节点 $1$ 为“仄声”，指定节点 $2$ 为“平声”的方案均不符合题意，因为这会使从根节点到节点 $3$ 的简单路径上依次经过的节点 $1$、节点 $2$、节点 $3$ 构成“孤平”。 需要注意的是，本题中，我们不关心不在根节点到“关键点”路径上的点的平仄使用情况是否符合题意。例如，方案 $6$ 的节点 $2$、节点 $4$、节点 $5$ 依次被指定为“仄声”、“平声”、“仄声”，会构成“孤平”，但由于不存在一条从根节点到一“关键点”的简单路径同时包含这三个节点，因此，这个方案也符合题意。 第二次练习只选取节点 $1$ 为“关键点”，指定为“平声”。此时，剩余五个节点的平仄都可以任意指定。故此次练习共有 $2^5 = 32$ 种方案。 第三次练习选取节点 $2$、节点 $4$、节点 $5$ 为“关键点”，分别指定为“仄声”、“平声”、“仄声”。此时，无论如何指定剩余节点的平仄，在根节点到节点 $5$ 的路径上总会依次经过节点 $2$、节点 $4$、节点 $5$ 构成“孤平”。故此次练习不存在任何方案。 对于样例二，除输出参数外与样例一没有任何区别。此时应输出 $\left\lfloor\dfrac{3}{2}\right\rfloor = 1$ 行，这一行应输出第一次与第二次练习的方案数的异或和，故输出 $12 \otimes 32 = 44$。 ### 数据规模与约束 **本题采用捆绑测试** 对于 $100\%$ 的数据，有 $1 \le n \le 5 \times 10^5$，$1 \le t,q \le 5 \times 10^5$，$\left\lfloor\dfrac{t}{q}\right\rfloor \le 5 \times 10^4$。对于 $\forall 1 \le i \le t$，有 $1 \le k_i \le n$，且 $\sum\limits_{i=1}^t k_i \le 5 \times 10^5$。对于 $\forall 1\le j \le k_i$，有 $1 \le p_{i,j} \le n$，$s_{i,j} \in \{0,1\}$，同一次练习中所有的 $p_{i,j}$ 互不相同。保证给出的是一棵树。 | Subtask 编号 | 分值 | $t$ | $n$ | $\sum k$ |特殊性质 | | :----------: | :--: | :-: | :-: | :-: |:------: | | $0$ | $8$ | $\le 20$ | $\le 20$ | $\le 200$ | 不符合 | | $1$ | $16$ | $\le 200$ | $\le 10^5$ | $\le 200$ | 符合 | | $2$ | $16$ | $\le 10^5$ | $\le 5 \times 10^5$ | $\le 10^5$ | 符合 | | $3$ | $8$ | $\le 5 \times 10^5$ | $\le 5 \times 10^5$ | $\le 5 \times 10^5$ | 符合 | | $4$ | $20$ | $\le 200$ | $\le 10^5$ | $\le 10^5$ | 不符合 | | $5$ | $24$ | $\le 10^5$ | $\le 5 \times 10^5$ | $\le 10^5$ | 不符合 | | $6$ | $8$ | $\le 5 \times 10^5$ | $\le 5 \times 10^5$ | $\le 5 \times 10^5$ | 不符合 | 对于符合特殊性质的测试点，保证 $\forall 1 \le i \le t$，有 $k_i = 1$。