P13255 [GCJ 2014 #1C] Enclosure

Your task in this problem is to find out the minimum number of stones needed to place on an $N$-by-$M$ rectangular grid ($N$ horizontal line segments and $M$ vertical line segments) to enclose at least $K$ intersection points. An intersection point is enclosed if either of the following conditions is true: 1. A stone is placed at the point. 2. Starting from the point, we cannot trace a path along grid lines to reach an empty point on the grid border through empty intersection points only. 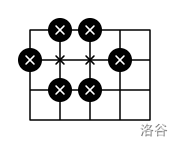For example, to enclose $8$ points on a $4\times 5$ grid, we need at least $6$ stones. One of many valid stone layouts is shown below. Enclosed points are marked with an "x". 

The first line of the input gives the number of test cases, $T$. $T$ lines follow. Each test case is a line of three integers: $N$ $M$ $K$.

For each test case, output one line containing "Case #$x$: $y$", where $x$ is the test case number (starting from 1) and $y$ is the minimum number of stones needed.

**Sample Explanation** - $1 \leq T \leq 100$. - $1 \leq N$. - $1 \leq M$. - $1 \leq K \leq N \times M$. **Small dataset(15 Pts)** - Time limit: ~~60~~ 3 seconds. - $N \times M \leq 20$. **Large dataset(30 Pts)** - Time limit: ~~120~~ 10 seconds. - $N \times M \leq 1000$.