P13266 [GCJ 2014 Finals] Symmetric Trees
题目描述
给定一棵**顶点有颜色**的树,判断它能否在二维平面中绘制成具有**对称轴**的图形。
更正式地说,一棵树被称为“轴对称”的,当且仅当存在一种顶点在二维平面中的坐标分配方式,使得:
- 所有顶点的坐标都互不相同;
- 如果某个顶点 $\mathbf{v}_i$ 的颜色为 $\mathbf{C}$,坐标为 $(x_i, y_i)$,那么必须存在另一个顶点 $\mathbf{v}_i'$,其颜色也为 $\mathbf{C}$,坐标为 $(-x_i, y_i)$。特别注意:如果 $x_i = 0$,那么 $\mathbf{v}_i$ 自身就是它的对称点;
- 对于任意一条边 $(\mathbf{v}_i, \mathbf{v}_j)$,也必须存在一条边 $(\mathbf{v}_i', \mathbf{v}_j')$;
- 如果我们将边绘制为直线段,则任意两条边**只能在公共端点处重合**,不能在其他地方相交。
现在请你判断,给定的每棵树是否满足上述“轴对称”条件。
输入格式
第一行是测试用例数量 $\mathrm{T}$。
接下来是 $\mathrm{T}$ 个测试用例。
每个测试用例格式如下:
- 第一行一个整数 $\mathrm{N}$,表示树中顶点数量;
- 接下来 $\mathrm{N}$ 行中,每行一个大写字母,表示第 $i$ 个顶点的颜色;
- 然后是 $\mathrm{N} - 1$ 行,每行两个整数 $i, j$($1 \leq i < j \leq N$),表示树中存在一条从节点 $i$ 到节点 $j$ 的无向边。所有边构成一棵连通树。
输出格式
对于每个测试用例,输出一行,格式为 `"Case #x: y"`,其中 $x$ 是测试用例编号(从 1 开始),$y$ 为:
- `"SYMMETRIC"` 表示这棵树可以绘制成具有对称轴的图;
- `"NOT SYMMETRIC"` 表示不可能具有对称轴。
说明/提示
**样例解释**
第一个样例可以按照如下方式绘制,满足对称轴条件:
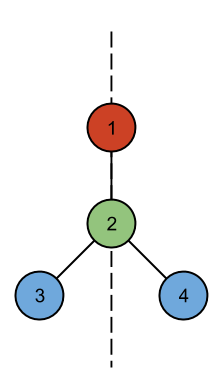
第二个样例无法找到任何符合对称要求的排列方式:
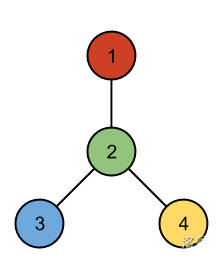
第三个样例中,有一种绘制方式满足关于一条垂直对称轴的对称关系:
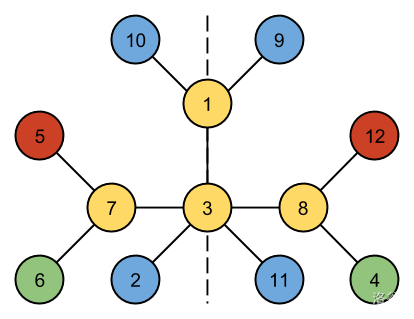
## 限制条件
- $1 \leq T \leq 100$
### Small 数据集(7 分)
- 时间限制:~~60~~ 3 秒
- $2 \leq N \leq 12$
### Large 数据集(18 分)
- 时间限制:~~120~~ 5 秒
- $2 \leq N \leq 10000$