P13279 「CZOI-R4」生长的树

你是小 J 的园丁，你需要帮他修剪他的一棵生长的树 $T_1$。 $T_1$ 是一棵 $k$ 叉树，在第 $0$ 个时刻，$T_1$ 只有**根节点**一个节点，编号为 $1$。 接下来从第 $1$ 个时刻开始，对于每 $1$ 个时刻将**依次**发生： - 当前的 $T_1$ 中所有儿子数量**小于** $k$ 个的节点，将补充若干个子节点使其儿子数量为 $k$，补充的节点的编号可以**任意决定（无需小于等于 $n$）**，但不可以与 $T_1$ 的其他节点的编号相同。 - 你进行若干次操作（可以不进行），每次操作指定 $T_1$ 的一个**不为根节点**的节点，将**它的子树**从 $T_1$ 上删除。 小 J 会给定你一棵有 $n$ 个节点的树 $T_2$，$T_2$ 的**根节点**编号为 $1$，他希望某个时刻后满足以下条件： - $T_1$ 有 $n$ 个节点，且节点的编号恰好为 $1\sim n$。 - 在 $T_1,T_2$ 中，除了根节点，所有**编号相同**的节点的父亲编号相同。 你需要求出最早可以在第几个时刻后满足条件，和在此基础上的**最小**操作次数。

第一行输入 $2$ 个整数 $n,k$。 接下来 $n-1$ 行，每行输入 $2$ 个整数 $u,v$，描述小 J 给定的树 $T_2$，表示编号为 $u,v$ 的节点有边相连。

第一行输出 $2$ 个整数 $p,q$，表示最早可以在第 $p$ 个时刻后满足条件，在此基础上**最少**操作次数为 $q$。

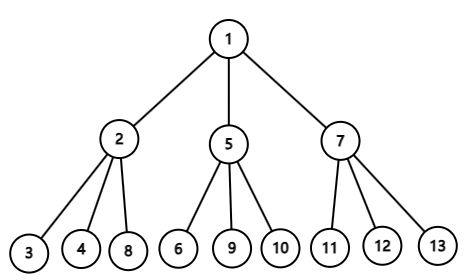
**【样例解释】** 如图，在第 $1,2$ 个时刻这样分配节点编号，并在 $2$ 个时刻时，删除编号为 $7,8,9,10$ 的节点的子树即可。可以证明不存在更优的答案。  **【数据范围】** **本题采用捆绑测试**。 - Subtask #1（$10\text{ pts}$）：$k=1$。 - Subtask #2（$10\text{ pts}$）：$T_2$ 是一棵满 $k$ 叉树。 - Subtask #3（$20\text{ pts}$）：$n,k\le10$。 - Subtask #4（$20\text{ pts}$）：$k=2$。 - Subtask #5（$40\text{ pts}$）：无特殊限制。 对于 $100\%$ 的数据，$1\le u,v\le n\le 5\times 10^5$，$1\le k\le 10^6$，$\max\limits_{1\le i\le n}\{\text{son}_i\}\le k$。其中 $\text{son}_i$ 指 $T_2$ 的第 $i$ 个节点的儿子**个数**。