P13279 Growing Tree

You are Little J's gardener, and you need to help him prune his growing tree, $T_1$. $T_1$ is a $k$-ary tree. At time 0, $T_1$ consists of only the root node with ID 1. Starting from time 1, at each time step, the following events occur in order: - **Growth Phase**: For all nodes in $T_1$ that have fewer than $k$ children, new child nodes are added until they have exactly $k$ children. The IDs of these new nodes can be arbitrarily assigned (they don't need to be $\le n$), but must be unique within $T_1$. - **Pruning Phase**: You may perform any number of operations (including zero), where each operation consists of selecting any non-root node of $T_1$ and removing its entire subtree. Little J provides you with a tree $T_2$ of $n$ nodes (rooted at node 1). The goal is to satisfy the following conditions after some time: - $T_1$ must have exactly $n$ nodes with IDs exactly 1 through $n$. - For all non-root nodes, nodes with the same ID in $T_1$ and $T_2$ must have the same parent. Your task is to determine: - The earliest time $p$ when these conditions can be satisfied. - The minimum number of pruning operations $q$ required at that time.

First line: Two integers $n$ and $k$. Next $n-1$ lines: Pairs $(u,v)$ describing edges of $T_2$.

Two space-separated integers $p$ $q$: 1. Earliest possible time $p$ to satisfy conditions. 2. Minimum operations $q$ needed at time $p$.

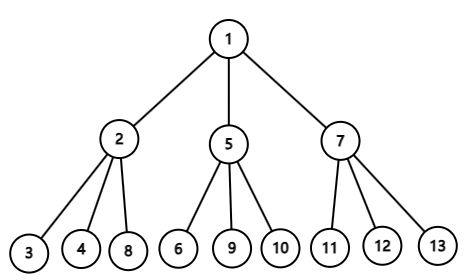
**Sample Explanation:** As shown in the figure, after assigning node IDs at times $1$ and $2$, and then deleting subtrees of nodes $7,8,9,10$ at time $2$, the conditions are satisfied. It can be proven that no better solution exists.  **Data Range** **This problem uses bundled testing:** - Subtask#1 ($10\ \text{pts}$): $k=1$. - Subtask#2 ($10\ \text{pts}$): $T_2$ is a perfect $k$-ary tree.(That means every non-leaf nodes have $k$ children.) - Subtask#3 ($20\ \text{pts}$): $n,k≤10$. - Subtask#4 ($20\ \text{pts}$): $k=2$. - Subtask#5 ($40\ \text{pts}$): No additional constraints. For all data $1\le u,v\le n\le5\times10^5$, $1\le k\le10^6$, $\max\limits_{1\le i\le n}\{son_i\}\le k$. Here, $son_i$ refers to the **number of sons** of the $i$-th node in $T_2$.