P1328 [NOIP 2014 Senior] Rock-Paper-Scissors-Lizard-Spock

NOIP 2014 Senior D1T1.

Rock-paper-scissors is a common hand game: rock beats scissors, scissors beat paper, and paper beats rock. If two players show the same gesture, it is a draw. In Season 2, Episode 8 of “The Big Bang Theory,” an upgraded version of the game appears. On top of the traditional rock-paper-scissors game, the upgraded version adds two new gestures: Spock: one of the main characters in Star Trek. Lizard: a villain in Star Trek. The win–loss relationships among the five gestures are shown in Table 1. The table lists the result of player A versus player B.  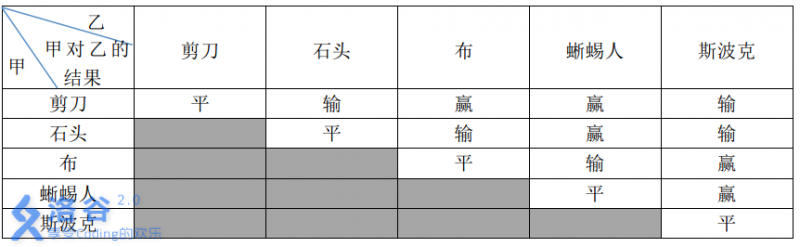Now, Xiao A and Xiao B are trying this upgraded hand game. It is known that their moves follow periodic patterns, though their period lengths may differ. For example: if Xiao A plays with the period `石头-布-石头-剪刀-蜥蜴人-斯波克` of length $6$, then his sequence of moves is `石头-布-石头-剪刀-蜥蜴人-斯波克-石头-布-石头-剪刀-蜥蜴人-斯波克-...`; and if Xiao B plays with the period `剪刀-石头-布-斯波克-蜥蜴人` of length $5$, then his sequence of moves is `剪刀-石头-布-斯波克-蜥蜴人-剪刀-石头-布-斯波克-蜥蜴人-...`. They will play a total of $N$ rounds. In each round, the winner gets $1$ point, the loser gets $0$ points; in a draw, both get $0$ points. Please compute the scores of the two players after $N$ rounds.

The first line contains three integers: $N, N_A, N_B$, representing the total number of rounds, the period length of Xiao A’s moves, and the period length of Xiao B’s moves, respectively. The numbers are separated by a space. The second line contains $N_A$ integers representing Xiao A’s pattern, and the third line contains $N_B$ integers representing Xiao B’s pattern. Here, $0$ denotes `剪刀`, $1$ denotes `石头`, $2$ denotes `布`, $3$ denotes `蜥蜴人`, and $4$ denotes `斯波克`. The numbers are separated by a space.

Output a single line containing two integers separated by a space, representing the scores of Xiao A and Xiao B, respectively.

For $100\%$ of the testdata, $0 < N \leq 200, 0 < N_A \leq 200, 0 < N_B \leq 200$. Translated by ChatGPT 5