P13295 [GCJ 2013 #2] Many Prizes

We're going to run a tournament with $2^N$ teams, and give out $P$ identical prizes to the teams with ranks $0\dots P-1$. The teams are numbered $0$ through $2^N-1$. When team $i$ and team $j$ play against each other in a game, team $i$ will win iff $i < j$. The teams for a tournament are organized in some order, called the tournament's tournament list, which contains all $2^N$ teams in the tournament. The tournament list will affect which teams play each other, and in what order. Your job will be to find the largest-numbered team that is guaranteed to win a prize, independent of how the tournament list is ordered; and to find the largest-numbered team that could win a prize, depending on how the tournament list is ordered. **Tournament Resolution** The tournament is conducted in $N$ rounds. Each team has a record: the list of the results of the games it has played so far. For example, if a team has played three games, and won the first, lost the second and won the third, its record is $[W, L, W]$. If a team has played zero games, its record is $[]$. In each round, every team plays a game against a team with the same record. The first team in the tournament list with a particular record will play against the second team with that record; the third team with the same record will play against the fourth; and so on. After $N$ rounds, each team has a different record. The teams are ranked in reverse lexicographical order of their records; so $[W, W, W] > [W, W, L] > [W, L, W] > [L, L, L]$. Here is an example of a tournament with $N=3$, and the tournament list $[2, 4, 5, 3, 6, 7, 1, 0]$, where the columns represent different rounds, and the teams are grouped by their records. The winner of each game in the example has been marked with a $*$.  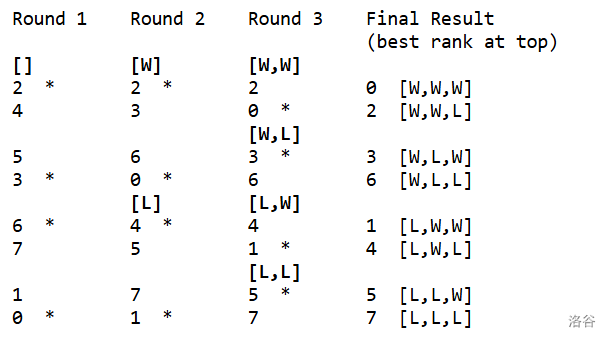If we give out $4$ prizes ($N=3, P=4$), the prizes will go to teams $0$, $2$, $3$ and $6$. The largest-numbered team that was guaranteed to win a prize with $N=3, P=4$, independent of the order of the tournament list, was team $0$: this tournament list demonstrated that it's possible for team $1$ not to win a prize, and it turns out that team $0$ will always win one, regardless of the order of the tournament list. The largest-numbered team that could win a prize with $N=3, P=4$, depending on how the tournament list was ordered, was team $6$: this tournament list demonstrated that it's possible for team $6$ to win a prize, and it turns out that team $7$ will never win one, regardless of the order of the tournament list.

The first line of the input gives the number of test cases, $T$. $T$ test cases follow. Each test case consists of two space-separated integers: $N$, which indicates the tournament has $2^N$ teams, and $P$, the number of prizes.

For each test case, output one line containing "Case #x: y z", where $x$ is the case number (starting from 1), $y$ is the largest-numbered team that is guaranteed to win a prize, independent of how the tournament list is ordered; and $z$ is the largest-numbered team that could win a prize, depending on how the tournament list is ordered.

**Limits** * $1 \leq T \leq 100$. * $1 \leq P \leq 2^N$. **Small dataset (7 Pts, Test set 1 - Visible)** * $1 \leq N \leq 10$. **Large dataset (13 Pts, Test set 2 - Hidden)** * $1 \leq N \leq 50$.