P13297 [GCJ 2013 #2] Multiplayer Pong

有两队玩家在玩乒乓球（pong）。Pong 是一款简单的电子游戏，每名玩家控制一个球拍（在本题中我们假设球拍是一个点），一颗小球在场地上来回弹跳。每队的球员需要按照固定的循环顺序击球（例如三人队时，第一次击球的是 P1，然后是 P2，然后是 P3，然后又轮到 P1），直到某名球员没能接住球，球就会飞出场地，该球员所在的队伍输掉比赛。 更准确地说：比赛场地是一个 $A \times B$ 的矩形。每个竖直边（长度为 $A$）上有若干球拍，每名球员守卫一侧，球拍为一个点。每队所有球员的球拍可以以相同的速度在竖直方向移动（以每秒多少单位计），且可以自由穿过彼此。场上还有一颗球，给定其初始位置（横坐标和纵坐标，均从左下角算起）和初始速度（横向和纵向，单位为每秒多少单位）。球员可以在知道球的初始位置后自由选择自己球拍的初始位置。每当球撞到水平边界时，会发生反弹（入射角等于反射角）。每当球撞到场地的竖直边界时，如果当前轮到的球员的球拍正好在该位置，球会反弹；如果没有，则本轮应该接球的球员所在队伍输掉比赛。 比赛可能会持续很长时间，球会在两队之间不断来回弹跳。你的目标是判断比赛的最终结果（假设所有球员都采取最优策略）。

输入的第一行为测试用例数 $T$。接下来有 $T$ 个测试用例，每个测试用例包含四行。第一行包含两个整数 $A$ 和 $B$，表示场地的高和宽。第二行包含两个整数 $N$ 和 $M$，分别表示守卫 $X = 0$ 侧的球员数和守卫 $X = B$ 侧的球员数。第三行包含两个整数 $V$ 和 $W$，分别表示两队球员球拍的速度。第四行包含四个整数：$Y, X, V_Y, V_X$，分别表示球的初始位置（纵坐标 $Y$、横坐标 $X$）和初始速度（纵向 $V_Y$、横向 $V_X$，每秒单位数，球最初向右）。

对于每个测试用例，输出一行 `"Case #x: y"`，其中 $x$ 是测试用例编号（从 $1$ 开始），$y$ 有三种可能的输出： - `"DRAW"`：如果比赛可以无限进行下去，永远不会分出胜负； - `"LEFT z"`：如果 $X = 0$ 一侧的队伍获胜，且对方最多能成功接球 $z$ 次； - `"RIGHT z"`：如果 $X = B$ 一侧的队伍获胜，且对方最多能成功接球 $z$ 次。

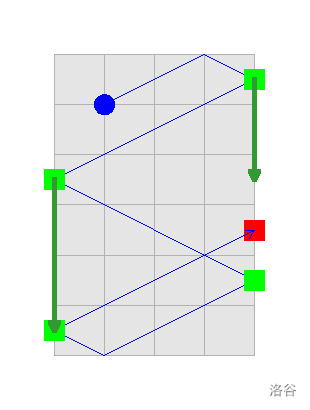
**样例说明**  上图展示了第一个样例的比赛过程。球在 $0.375$ 秒时撞到右侧边界（此时第一个 RIGHT 队员可以接球，比如一开始就把球拍放在那里并保持不动），在 $0.875$ 秒时撞到左侧边界（LEFT 队员接球），$1.375$ 秒时再次撞到右侧（第二个 RIGHT 队员可以提前到达反弹点），然后又回到左侧（LEFT 队员刚好能及时赶到——她需要在 1 秒内跑完 3 个单位距离），接着球撞到右侧边界时，第一个 RIGHT 队员无法及时赶到。注意，第二个 RIGHT 队员虽然能接到球，但根据规则不能越位。还要注意，如果 RIGHT 队再多一名队员，就能接到球，LEFT 就会输——球会飞得太高，LEFT 队员无法及时赶到。 **限制条件** - $1 \leq T \leq 100$ - $0 < X < B$ - $0 < Y < A$ **小数据集（12 分，测试集 1 - 可见）** - $1 \leq N, M \leq 10^6$ - $1 \leq V, W \leq 10^{12}$ - $-10^{12} \leq V_Y \leq 10^{12}$ - $-10^6 \leq V_X \leq 10^6$ - $2 \leq A, B \leq 10^6$ **大数据集（25 分，测试集 2 - 隐藏）** - $1 \leq N, M \leq 10^{100}$ - $1 \leq V, W \leq 10^{100}$ - $-10^{100} \leq V_Y, V_X \leq 10^{100}$ - $2 \leq A, B \leq 10^{100}$ 翻译由 ChatGPT-4.1 完成。