P13302 [GCJ 2013 Finals] Graduation Requirements

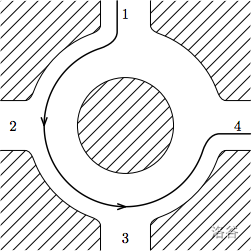
在 Awesome Programmer University 毕业之前，学生们传统上需要完成一些“毕业要求”。其中一项就是逆行绕环形交通岛驾驶一圈。对大多数人来说，这已经够疯狂了，但作为额外挑战，你还想看看自己是否能不停歇地逆行绕交通岛转好几圈。 这个环形交通岛共有 $N$ 个路口，等距分布于圆周上。正常情况下，汽车会在某个路口进入环岛，然后每秒逆时针行驶到下一个路口，最终到达目的地并驶离环岛。  你已经观察了 $X$ 秒内所有进入和离开环岛的汽车。对于每辆车，你都记录了它进入环岛的时间，以及它进出环岛的路口编号。所有汽车都以每秒 1 个路口的速度逆时针行驶。你观察到的每辆车都会在回到其进入路口之前离开环岛。环岛上有多条车道，因此同一时刻可以有多辆车占据同一位置。 如果你能合理规划，最大能在这段时间内顺时针在环岛上行驶多久？你必须在某个整数时刻（$\geq 0$）进入环岛，在时间 $\leq X$ 时离开，并且一旦离开就不能再回来。在环岛上，你必须以每秒 1 个路口的速度顺时针行驶。你希望尽可能安全（当然，逆行本身就很危险），因此你绝不能与任何其他车辆相遇或擦肩而过。特别地，你不能在某一时刻从有其他车辆进入的路口驶出，也不能在有其他车辆离开的路口驶入。你可以自由选择何时何地进入和离开环岛。

输入的第一行为测试用例数 $T$。接下来有 $T$ 组测试数据。每组数据第一行为你观察到的车辆数 $C$。第二行为两个整数 $X$ 和 $N$，分别表示你观察的时间（秒数）和环岛上的路口数。接下来的 $C$ 行，每行三个整数 $s_i$、$e_i$ 和 $t_i$，表示一辆车在 $t_i$ 时刻从 $s_i$ 号路口进入，在某一时刻从 $e_i$ 号路口离开。路口编号为 $1$ 到 $N$，按逆时针方向编号（即 $2$ 号路口在 $1$ 号路口的逆时针下一个位置）。

对于每个测试用例，输出一行 `"Case #x: y"`，其中 $x$ 为测试用例编号（从 1 开始），$y$ 为你能顺时针行驶的最长秒数。注意，如果你无法进入环岛，或者即使进入也无法行驶一格路口，$y$ 也可以为 $0$。 注意，你必须在整数秒数时刻进入环岛，也就是说，你每到达一个路口时刻都必须是整数。

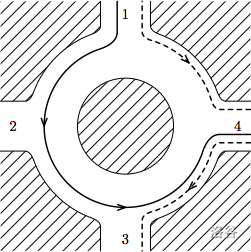
**样例说明** 在第一个样例中，有一辆车，其行驶路线如题图所示。有多种方式可以让你逆行 1 秒，例如你可以在第 1 号路口的第 1 秒进入（不能在第 0 秒进入，因为那时有车在那里），然后行驶到第 4 号路口（不能继续前进到第 3 号路口，因为会与从 3 号行驶到 4 号的车相遇）。另一种方式是第 0 秒在第 4 号路口进入，行驶到第 3 号路口后离开。  在第二个样例中，你可以在第 1 秒从第 5 号路口进入，逆行到第 3 号路口，总共顺时针行驶 2 秒。第三个样例中，你无法进入环岛——每一秒所有路口都有车。第四个样例没有任何车辆，因此你可以在任意时刻、任意路口进入，从 0 秒开始一直顺时针行驶到第 6 秒。第五个样例中虽然可以进入环岛，但由于只有 3 个路口，无论如何都会与其他车相遇，因此无法顺时针前进一格。 注意：现实中逆行环岛极其危险，可能伤及自己或他人。Google（以及 Google Code Jam）强烈建议你不要尝试此类行为。 **限制条件** - $1 \leq T \leq 100$ - $1 \leq s_i, e_i \leq N$ - $s_i \neq e_i$ - $0 \leq t_i$ - 每辆车都在 $X$ 秒内或更早驶离环岛。 **小数据集（7 分，测试集 1 - 可见）** - $3 \leq N \leq 10$ - $1 \leq X \leq 10$ - $0 \leq C \leq 10$ **大数据集（18 分，测试集 2 - 隐藏）** - $3 \leq N \leq 10^{10}$ - $1 \leq X \leq 10^{10}$ - $0 \leq C \leq 1000$ 翻译由 ChatGPT-4.1 完成。