P13310 Empurple

[エンパープル](https://music.163.com/#/song?id=2690902320)。 > Please,Forgive me and "Purple" > > まだ真ん中の私Empurple

Yuki has a tree of size $n$. Yuki defines the weight of a tree coloring scheme as follows: Let $a$ be the sum of the squares of the sizes of all red maximal connected components. Let $b$ be the sum of the squares of the sizes of all blue maximal connected components. The weight of this coloring scheme is $ab$. Some nodes on the tree have already been colored red or blue. Color the remaining nodes red or blue, and find the sum of the weights of all valid coloring schemes. Let the number of nodes to be colored be $C$. Then there are $2^C$ valid coloring schemes in total. The answer may be very large, so please modulo $998244353$.

The first line inputs an integer $n$. The next $n-1$ lines each contain two integers $u_i$ and $v_i$, representing an edge $(u_i, v_i)$ on the tree. The next line contains a string $s$ of $n$ characters. When $s_i=\texttt{r}$, the node is red. When $s_i=\texttt{b}$, the node is blue. When $s_i=\texttt{w}$, the node is to be colored.

Output the answer modulo $998244353$.

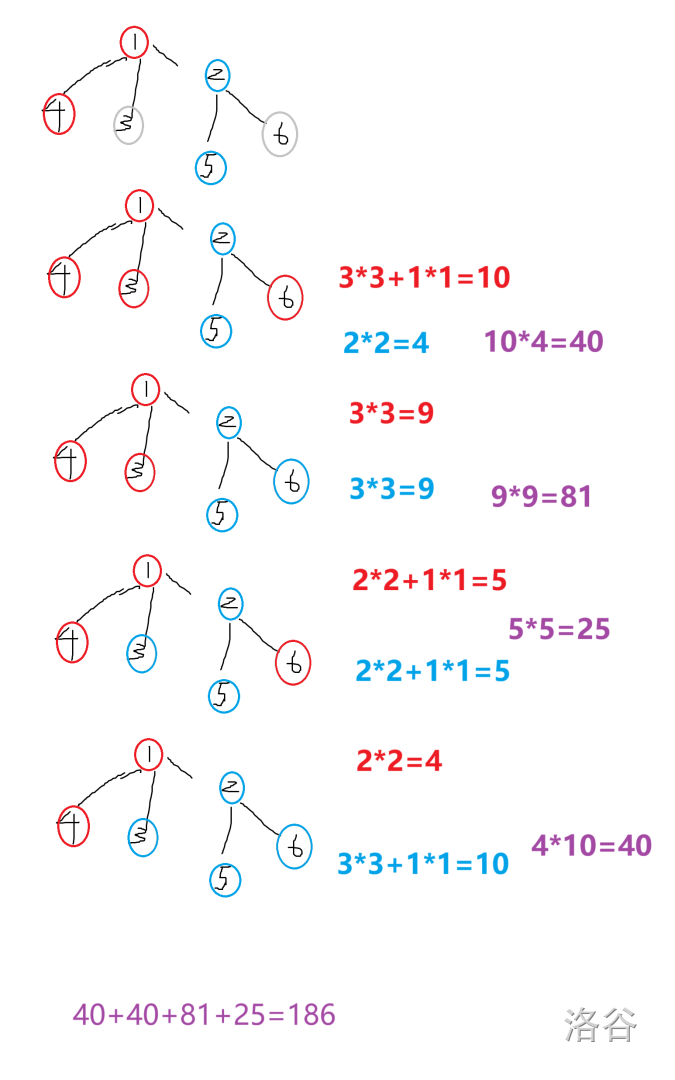
Sample 1 explanation:  ## Test Case Distribution | ID | Points | Range of $n$ | Special Properties | | :-----------: | :-----------: | :-----------: | :-----------: | | 0 | 10 | $n \le 10$ | | | 1 | 10 | $n \le 40$ | $s_i =\texttt{w}$ | | 2 | 10 | $n \le 300$ | | | 3 | 10 | $n \le 5000$ | | | 4 | 10 | $n \le 10^6$ | $s_i \in \{\texttt{r},\texttt{b}\}$ | | 5 | 10 | $n \le 2\times 10^5$ | $s_i \in \{\texttt{r},\texttt{w}\}$ | | 6 | 10 | $n \le 2\times 10^5$ | $s_i =\texttt{w}$ | | 7 | 10 | $n \le 2\times 10^6$ | $u_i=v_i-1$ | | 8 | 10 | $n \le 10^6$ | $u_i=1$ | | 9 | 10 | $n \le 2\times 10^6$ | | For all data: $1\le n \le 2\times 10^6$, $s_i \in \{\texttt{r},\texttt{w},\texttt{b}\}$, $1\le u_i,v_i\le n$.