P13321 [GCJ 2012 #1C] Diamond Inheritance

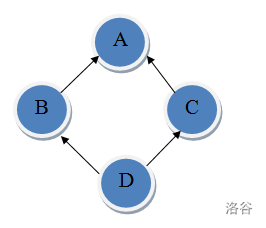
You are asked to help diagnose class diagrams to identify instances of diamond inheritance. The following example class diagram illustrates the property of diamond inheritance. There are four classes: $A, B, C$ and $D$. An arrow pointing from $X$ to $Y$ indicates that class $X$ inherits from class $Y$.  In this class diagram, $D$ inherits from both $B$ and $C$, $B$ inherits from $A$, and $C$ also inherits from $A$. An inheritance path from $X$ to $Y$ is defined as a sequence of classes $X$, $C_1$, $C_2$, $C_3$, $\dots$, $C_n$, $Y$ where $X$ inherits from $C_1$, $C_i$ inherits from $C_{i+1}$ for $1 \leq i \leq n - 1$, and $C_n$ inherits from $Y$. There are two inheritance paths from $D$ to $A$ in the example above. The first path is $D$, $B$, $A$ and the second path is $D$, $C$, $A$. A class diagram is said to contain a diamond inheritance if there exists a pair of classes $X$ and $Y$ such that there are at least two different inheritance paths from $X$ to $Y$. The above class diagram is a classic example of diamond inheritance. Your task is to determine whether or not a given class diagram contains a diamond inheritance.

The first line of the input gives the number of test cases, $T$. $T$ test cases follow, each specifies a class diagram. The first line of each test case gives the number of classes in this diagram, $N$. The classes are numbered from $1$ to $N$. $N$ lines follow. The $i^{th}$ line starts with a non-negative integer $M_i$ indicating the number of classes that class $i$ inherits from. This is followed by $M_i$ distinct positive integers each from $1$ to $N$ representing those classes. You may assume that: * If there is an inheritance path from $X$ to $Y$ then there is no inheritance path from $Y$ to $X$. * A class will never inherit from itself.

For each diagram, output one line containing "Case #$x$: $y$", where $x$ is the case number (starting from $1$) and $y$ is "Yes" if the class diagram contains a diamond inheritance, "No" otherwise.

**Limits** - $1 \leq T \leq 50$. - $0 \leq M_i \leq 10$. **Test set 1 (14 Pts, Visible Verdict)** - $1 \leq N \leq 50$. **Test set 2 (14 Pts, Hidden Verdict)** - $1 \leq N \leq 1,000$.