P13335 [GCJ 2012 Finals] Twirling Towards Freedom

> "I say we must move forward, not backward; upward, not forward; > and always twirling, twirling, twirling towards freedom!" > — Former U.S. Presidential nominee Kodos.

After hearing this inspirational quote from America's first presidential nominee from the planet Rigel VII, you have decided that you too would like to twirl (rotate) towards freedom. For the purposes of this problem, you can think of "freedom" as being as far away from your starting location as possible. The galaxy is a two-dimensional plane. Your space ship starts at the origin, position $(0, 0)$. There are $N$ stars in the galaxy. Every minute, you can choose a star and rotate your space ship 90 degrees clockwise around the star. You may also choose to stay where you are. How far away can you move from the origin after $M$ minutes?  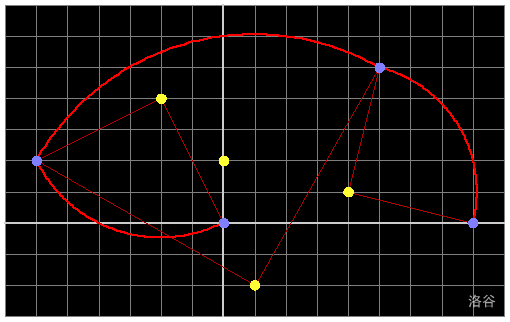The image illustrates the first 3 rotations for a possible path in sample case 1. Note that this path is not necessarily a part of any optimal solution.

The first line of the input gives the number of test cases, $T$. $T$ test cases follow, beginning with two lines containing integers $N$ and $M$. The next $N$ lines each contain two integers, $X_i$ and $Y_i$, representing the locations of stars.

For each test case, output one line containing "Case #$x$: $D$", where $x$ is the case number (starting from 1) and $D$ is the distance from the origin to the optimal final position. Answers with absolute or relative error no larger than $10^{-6}$ will be accepted.

**Limits** - $1 \leq T \leq 100;$ - $-1000 \leq X_i \leq 1000;$ - $-1000 \leq Y_i \leq 1000.$ - No two stars will be at the same location. - There may be a star at the origin. **Test set 1 (10 Pts, Visible Verdict)** - Time limit: ~~30~~ 3 seconds. - $1 \leq N \leq 10.$ - $1 \leq M \leq 10.$ **Test set 2 (39 Pts, Hidden Verdict)** - Time limit: ~~60~~ 6 seconds. - $1 \leq N \leq 5000.$ - $1 \leq M \leq 10^8.$