P13335 [GCJ 2012 Finals] Twirling Towards Freedom
题目背景
> “我说我们必须向前进,而不是向后退;
> 向上,而不是向前;
> 并且永远旋转、旋转、旋转走向自由!”
> ——前美国总统候选人 Kodos
题目描述
在听到来自 Rigel VII 星球美国首位总统候选人的这句激励人心的名言后,你也决定要旋转(即绕点旋转)走向自由。对于本题而言,你可以认为“自由”就是距离起点越远越好。
银河系是一个二维平面。你的宇宙飞船起始于原点 $(0, 0)$。银河中有 $N$ 颗恒星。每过一分钟,你可以选择一颗恒星,并绕该恒星顺时针旋转 $90$ 度;你也可以选择停留在原地不动。
经过 $M$ 分钟后,你最多能离原点多远?
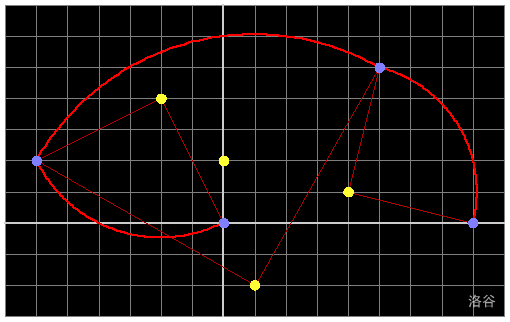
上图展示了样例第 1 组数据中某一条路径的前三次旋转。注意,这条路径不一定属于最优解的某一部分。
输入格式
输入的第一行为测试用例数 $T$。接下来有 $T$ 组测试数据,每组首先两行,包含整数 $N$ 和 $M$。接下来 $N$ 行,每行两个整数 $X_i$ 和 $Y_i$,表示一颗恒星的位置。
输出格式
对于每个测试用例,输出一行 "Case #$x$: $D$",其中 $x$ 为测试用例编号(从 1 开始),$D$ 为距离原点的最优最终距离。答案的绝对或相对误差不超过 $10^{-6}$ 即视为正确。
说明/提示
**限制条件**
- $1 \leq T \leq 100$
- $-1000 \leq X_i \leq 1000$
- $-1000 \leq Y_i \leq 1000$
- 不会有两颗恒星位于同一位置
- 可能存在位于原点的恒星
**测试集 1(10 分,结果可见)**
- 时间限制:~~30~~ 3 秒
- $1 \leq N \leq 10$
- $1 \leq M \leq 10$
**测试集 2(39 分,结果隐藏)**
- 时间限制:~~60~~ 6 秒
- $1 \leq N \leq 5000$
- $1 \leq M \leq 10^8$
翻译由 ChatGPT-4.1 完成。