P13338 三角形面积并 加强版

[原题链接](https://www.luogu.com.cn/problem/P4406)

给定 $n$ 个非退化三角形 $\triangle A_i B_i C_i\ (1 \leq i \leq n)$，你的任务是计算这些三角形的并集面积。 一个三角形是**非退化**的，当且仅当它具有非零面积，即三角形的三个顶点 $A_i,B_i,C_i$ 是不同的且不共线。换句话说，点 $A_i,B_i,C_i$ 不在同一条直线上，由这三点构成的三角形不是退化的。 三角形的**并集面积**是至少被其中一个三角形覆盖的总面积。形式化地，三角形的并集面积是由这些三角形所占区域的并集所形成的区域的面积： $$ \text{Area}\left(\bigcup_{i=1}^n S_i\right) $$ 其中 $S_i$ 表示三角形 $\triangle A_i B_i C_i$ 所占的几何区域，$\text{Area}(S_i)$ 是该区域的面积。$\bigcup_{i=1}^n S_i$ 表示至少被其中一个三角形覆盖的区域。

每个测试文件中仅包含一个测试用例。 第一行包含一个整数 $n\ (1 \leq n \leq 10^3)$，表示三角形的数量。 接下来的 $n$ 行，每行包含六个整数 $x_1\ y_1\ x_2\ y_2\ x_3\ y_3\ (0 \leq |x|, |y| \leq 10^6)$，表示三角形 $\triangle A_i B_i C_i$ 的三个顶点的坐标。

输出一个实数，表示这些三角形的并集面积。你的答案的绝对误差或相对误差应小于 $10^{-6}$。当你的答案为 $a$，评测机的答案为 $b$，则当 $\frac{|a-b|}{\max(1,|b|)} \leq 10^{-6}$ 时答案被接受。

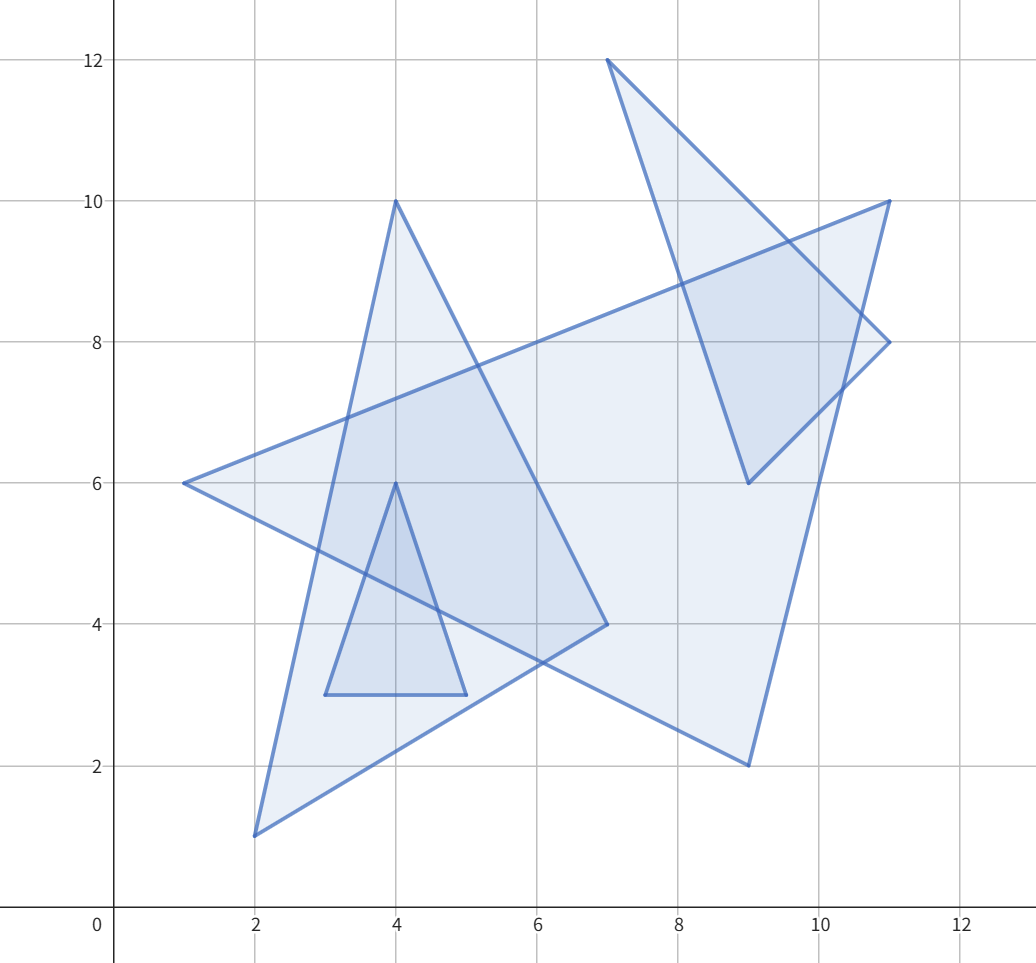
样例 2 图示：  对于子任务 1，输入数据满足 $1 \leq n \leq 100$，且 $0 \leq |x|, |y| \leq 10^3$。该子任务可用于测试算法的正确性。完成子任务 1 将获得总分的 $50\%$。 对于子任务 2，输入数据满足 $1 \leq n \leq 10^3$，且 $0 \leq |x|, |y| \leq 10^6$。完成子任务 2 将获得剩余 $50\%$ 的分数。 提示：求解三角形的并集面积是一个经典的 3SUM-hard 问题。你需要实现一个时间复杂度为 $\mathcal{O}(V^2 \log V)$ 的算法，其中 $V$ 为顶点总数。