P13343 [EGOI 2025] A String Problem / 一个弦线问题

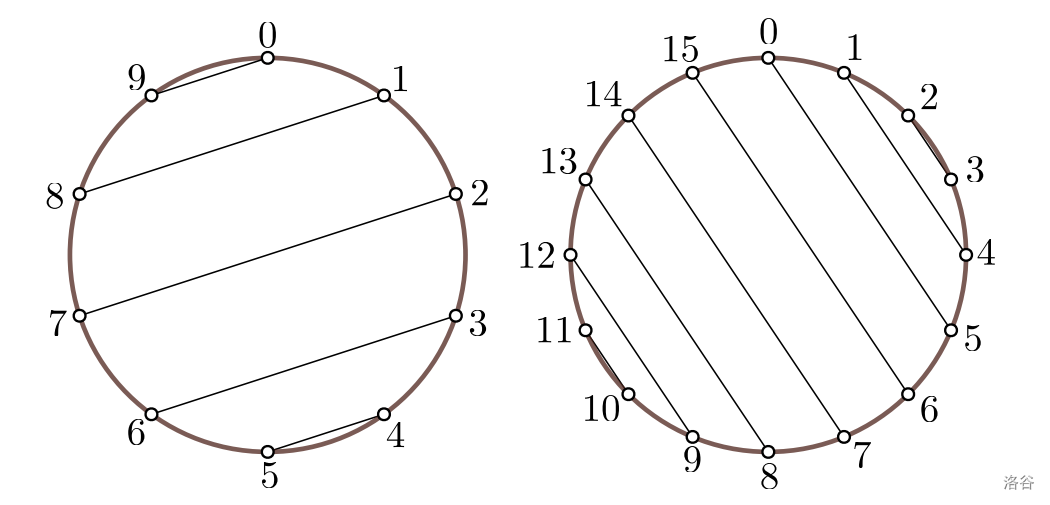
Lara 非常喜欢跳蚤市场。上周六，德国最大的跳蚤市场之一——Rheinaue-Flohmarkt 在波恩举办。Lara 一整天都在市场里闲逛、讨价还价，并买下了各种新奇的物品。她带回家中最有趣的东西是一把完全呈圆形的小型竖琴。当她准备弹奏时，发现琴弦的分布非常混乱，根本不是彼此平行的。 更具体地说，圆形琴框上均匀分布着 $2 \cdot N$ 个琴钉。每根琴弦都由两个琴钉固定，每个琴钉正好有一根琴弦连接。 Lara 对竖琴并不十分了解，但她很确定琴弦应该都平行排列。为了解决这个问题，她决定重新装配琴弦。每一步操作中，她可以将某根琴弦的一端从一个琴钉上取下，并重新连接到另一个琴钉。在操作过程中，允许多个琴弦的末端临时连接到同一个琴钉。最终，要求每个琴钉上正好有一根琴弦，并且所有 $N$ 根琴弦都平行。 下图给出了两种所有琴弦都平行的竖琴示例。  由于每次装配都非常耗时，Lara 希望用尽可能少的步骤完成。请帮她找出最少的操作步骤，并给出一种装配方案！

第一行输入一个整数 $N$，表示琴弦的数量。琴弦编号为 $0$ 到 $N-1$。 接下来 $N$ 行，第 $i$ 行（$0 \leq i \leq N-1$）包含两个整数 $a_i$ 和 $b_i$，表示第 $i$ 根琴弦当前固定在的两个琴钉上。所有琴钉顺时针编号为 $0$ 到 $2N-1$。每个琴钉正好有一根琴弦连接。

输出一个整数 $K$，表示为使所有琴弦平行所需的最少操作次数。 接下来输出 $K$ 行，每行三个整数 $p$、$s$ 和 $e$，表示在该步骤中，将第 $p$ 根琴弦从琴钉 $s$ 上取下并重新连接到琴钉 $e$ 上（$0 \leq p \leq N-1$，$0 \leq s, e \leq 2N-1$）。 注意，如果第 $p$ 根琴弦当前并未连接在 $s$ 上，则该操作序列无效。 若存在多种方案，输出任意一种即可。部分正确的答案也有可能获得部分分，详见下方说明。

### 样例说明 在第一个样例中，给出了一把有五根琴弦的竖琴。第一步，将第 $4$ 根琴弦从琴钉 $8$ 取下，重新连接到 $9$；第二步，将第 $0$ 根琴弦从 $5$ 取下，连接到 $8$；最后一步，将第 $1$ 根琴弦从 $9$ 取下，连接到 $5$。此时每个琴钉上正好有一根琴弦，且所有琴弦都平行。如下图所示：  下图展示了样例 2、3、4 的初始竖琴状态。  - 第 1 个样例满足测试组 4 和 5 的约束。 - 第 2 个样例满足测试组 1、3、4、5 的约束。 - 第 3 个样例满足测试组 2、4、5 的约束。 - 第 4 个样例满足测试组 3、4、5 的约束。 ### 约束与评分 * $4 \leq N \leq 100\,000$。 * $0 \leq a_i, b_i \leq 2N - 1$。 * 所有 $a_i$ 和 $b_i$ 互不相同。 你的解答将在一组测试组上进行评测，每组包含若干测试用例。每组得分规则如下： * 如果你的程序解决了该组所有测试用例，获得 $100\%$ 分数。 * 如果你的程序未能完全解决该组，但每个测试用例输出的 $K$ 都是最优的，则获得 $50\%$ 分数。 判断 $50\%$ 得分时，仅判定你输出的 $K$，可以只输出 $K$ 后直接退出，也可以输出一个无效的操作序列。你的程序仍需在时限内正确结束。 | 组别 | 分值 | 限制 | | :-: | :-: | :-: | | 1 | 14 | 对所有 $i$，第 $i$ 根琴弦固定在琴钉 $2i$ 和 $2i+1$ 上 | | 2 | 16 | 最多只需 2 步即可完成 | | 3 | 12 | 保证存在一种解法，使得有一根琴弦固定在琴钉 0 和 1 上 | | 4 | 28 | $N \leq 1000$ | | 5 | 30 | 无额外限制 | 翻译由 ChatGPT-4.1 完成。