P13348 「ZYZ 2025」未选择的路

> 黄色的树林里分出两条路 / 可惜我不能同时去涉足 > 我在那路口久久伫立 / 我向着一条路极目望去 / 直到它消失在丛林深处 > > 但我却选了另外一条路 / 它荒草萋萋，十分幽寂 / 显得更诱人，更美丽 > 虽然在这条小路上 / 很少留下旅人的足迹 > > 那天清晨落叶满地 / 两条路都未经脚印污染 / 啊，留下一条路等改日再见 > 但我知道路径延绵无尽头 / 恐怕我难以再回返 > > 也许多少年后在某个地方 / 我将轻声叹息将往事回顾 > 一片树林里分出两条路 / 而我选择了人迹更少的一条 / 从此决定了我一生的道路 > > ——义务教育教科书语文人教版七年级下册《未选择的路》

在平面直角坐标系中，有一个 $n\times n$ 的网格，其最左下角的点坐标为 $(0,0)$，最右上角的点坐标为 $(n,n)$。有一个人最初站在 $(0,0)$ 的位置，要到达 $(n,n)$。他每一次移动可以沿某个方格的对角线移动，并称他**经过**了这个方格。 请你求出，在仅经过每个方格**至多**一次的情况下，他最多能经过多少方格，并给出一种可行的方案。 你可以参照样例解释中的图片理解题意。

输入的第一行包含一个正整数 $n$。

**本题采用 Special Judge，你只需要输出任意一种符合条件的方案。** 第一行输出一个整数 $k$，表示他最多能经过的方格数。 接下来 $k$ 行，其中的第 $i$ 行输出两个整数 $x_i,y_i$，代表第 $i$ 次移动后这个人所在位置的坐标。

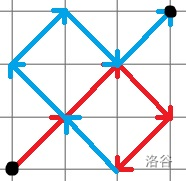
**【样例解释 #2】** 下图是输出所对应的方案，在可能会造成歧义的地方会走颜色相同的两条线段。  **【数据范围】** **本题采用捆绑测试。** |子任务编号|特殊性质|分值| |:-:|:-:|:-:| |$0$|$n\le6$|$30$| |$1$|$n$ 为奇数|$25$| |$2$|$n$ 为偶数|$25$| |$3$|无|$20$| 对于所有的测试数据，保证：$1\le n\le10^3$。