P13370 [GCJ 2011 #1B] House of Kittens

你最近收养了一些小猫，现在你想为它们建造一个房子。这个房子的外形是一个有 $N$ 个顶点的凸多边形。在房子的内部，会有 $M$ 条内部墙壁，沿直线连接顶点进行分隔。任意两条墙壁不会相交，但可能有多条墙壁连接到同一个顶点。 那么，为什么你的小猫房子如此特别呢？因为你将在每个顶点建造一个完全由猫薄荷制成的柱子！小猫们可以在它们所在房间内玩耍任何接触到该房间的柱子，这将给它们带来真正的豪华体验。 为了让房子更加有趣，你想使用不同口味的猫薄荷。每根柱子只能使用一种口味，但不同的柱子可以使用不同的口味。唯一的问题是：如果某个房间无法接触到所有在房子中使用的猫薄荷口味，那么在那个房间里的小猫就会感到被冷落而伤心。 你的任务是为每个顶点选择一种猫薄荷口味，使得（a）每个房间都能接触到所有的口味，（b）尽可能多地使用不同的口味。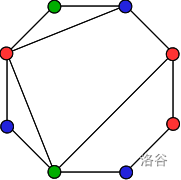 在下面的例子中，三种不同口味（用红色、绿色和蓝色点表示）被分布在一个八边形的房子上，同时保证每个房间里的小猫都能开心：  在上图中，从顶部墙的左角开始顺时针，颜色依次为：绿色、蓝色、红色、红色、蓝色、绿色、蓝色、红色。

第一行输入测试用例数 $T$。接下来有 $T$ 组测试数据。 每组测试数据包含三行。第一行包含两个整数 $N$ 和 $M$，分别表示顶点数和内部墙壁数。第二行包含 $M$ 个用空格分隔的整数 $U_1, U_2, \ldots, U_M$，表示每条内部墙壁的起点。第三行包含 $M$ 个用空格分隔的整数 $V_1, V_2, \ldots, V_M$，表示每条内部墙壁的终点。 更具体地说，如果房子的顶点按顺时针顺序编号为 $1, 2, \ldots, N$，则第 $i$ 条内部墙壁连接顶点 $U_i$ 和 $V_i$。

对于每组测试数据，输出两行。第一行输出 "Case #$x$: $C$"，其中 $x$ 是测试编号，$C$ 是可以使用的最大猫薄荷口味数。第二行输出 $N$ 个用空格分隔的整数 "$y_1$ $y_2$ ... $y_N$"，其中 $y_i$ 是分配给第 $i$ 个顶点的猫薄荷口味编号（$1$ 到 $C$ 之间的整数）。 如果存在多种分配方式都能达到 $C$ 种口味，可以输出任意一种。

**数据范围** - $1 \leq T \leq 100$。 - $1 \leq M \leq N - 3$。 - 对所有 $i$，$1 \leq U_i < V_i \leq N$。 - 内部墙壁之间不会相交，除非在 $N$ 个顶点处相交。 - 内部墙壁不会接触房子的外部，除非在 $N$ 个顶点处。 **小数据（20 分，测试点 1 - 可见）** - $4 \leq N \leq 8$。 - 时间限制：6 秒。 **大数据（25 分，测试点 2 - 隐藏）** - $4 \leq N \leq 2000$。 - 时间限制：12 秒。 由 ChatGPT 4.1 翻译