P13378 [GCJ 2011 #3] Irregular Cakes

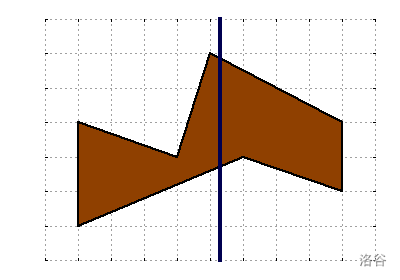
数学家 Mary 多年前创办了一家面包店，但经过这么长时间后，她已经厌倦了总是烘焙相同的矩形和圆形蛋糕。为了庆祝她的下一个生日，她想烤一个“不规则”蛋糕，这种蛋糕定义为 $x=0$ 到 $x=W$ 之间两条“折线”之间的区域。这两条折线分别称为下边界和上边界。  形式上，一条折线由一系列从左到右的点 $(P_0, P_1, \ldots, P_n)$ 定义。相邻的点通过线段连接，所有这些线段共同构成折线。 今天是 Mary 的生日，她已经烤好了一个由两条分别有 $L$ 个点和 $U$ 个点的折线围成的不规则蛋糕。在唱完“生日快乐”后，她想要做 $G-1$ 条竖直切割，将蛋糕分成 $G$ 份面积相等的蛋糕片，这样她就可以把蛋糕分给所有的客人。然而，不规则的蛋糕形状让这项任务变得相当棘手。你能帮她决定应该在哪里切割吗？

输入的第一行给出测试用例的数量 $T$。接下来有 $T$ 组测试数据。每组测试数据的第一行包含四个整数：$W$（蛋糕的宽度）、$L$（下边界的点数）、$U$（上边界的点数）以及 $G$（参加聚会的客人数）。 接下来 $L$ 行描述下边界。第 $i$ 行包含两个整数 $x_i$ 和 $y_i$，表示下边界第 $i$ 个点的坐标。再接下来 $U$ 行描述上边界。第 $j$ 行包含两个整数 $x_j$ 和 $y_j$，表示上边界第 $j$ 个点的坐标。

对于每个测试用例，输出 $G$ 行。第一行输出 “Case #$x$: ”，其中 $x$ 是测试用例编号（从 1 开始）。接下来的 $G-1$ 行，按从左到右的顺序输出每一刀的 $x$ 坐标。 只要答案的相对或绝对误差不超过 $10^{-6}$，就视为正确。

**数据范围** - $1 \leq T \leq 100$。 - $1 \leq W \leq 1000$。 - $2 \leq L \leq 100$。 - $2 \leq U \leq 100$。 - 所有坐标均为 $-1000$ 到 $1000$ 之间的整数。 - 两条边界的最左端点的 $x$ 坐标均为 $0$。 - 两条边界的最右端点的 $x$ 坐标均为 $W$。 - 同一条边界上的点按 $x$ 坐标递增排序。 - 同一条边界上的点的 $x$ 坐标互不相同。 - 对于所有 $x$，下边界始终严格在上边界之下（即下边界的 $y$ 坐标始终小于上边界的 $y$ 坐标）。 **小数据集（测试集 1 - 可见）** - $2 \leq G \leq 3$。 - 时间限制：3 秒。 **大数据集（测试集 2 - 隐藏）** - $2 \leq G \leq 101$。 - 时间限制：6 秒。 由 ChatGPT 4.1 翻译