P1337 [JSOI2004] Balance Point / Crushing XXX

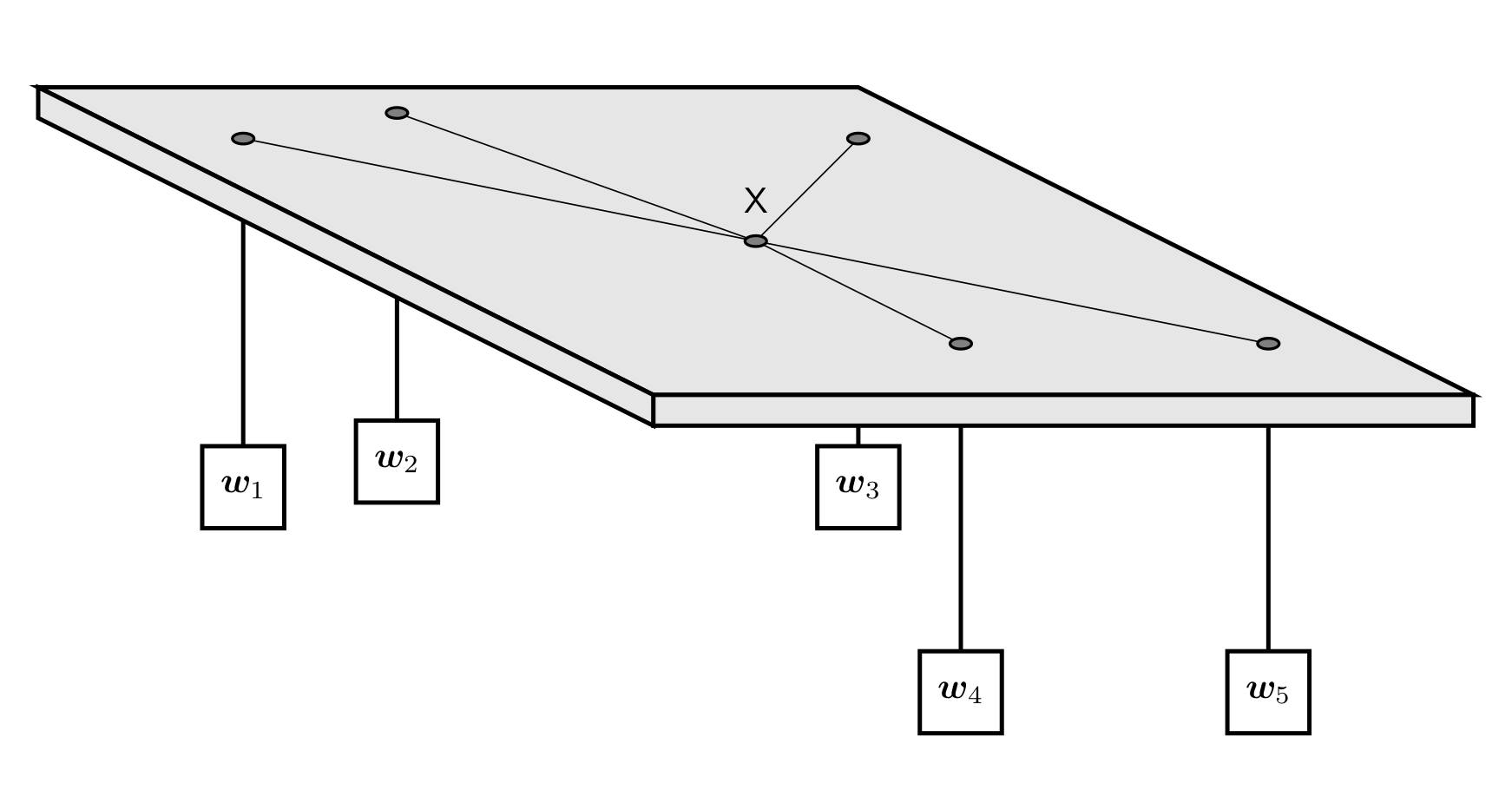
As shown in the figure, there are $n$ weights, each tied to a sufficiently long rope. Each rope passes from above through a hole on the tabletop and then they are tied together. The point $x$ in the figure is the common knot. Assume the ropes are perfectly elastic (i.e., cause no energy loss), the table is high enough (the weights will not reach the ground), and all friction is ignored. Find the final equilibrium position of the knot $x$. Note: The holes on the tabletop are much smaller than the knot $x$, so even if some weight is particularly heavy, the knot $x$ cannot pass through a hole and fall. At most, it will get stuck at the edge of some hole. 

The first line of the file is a positive integer $n$ ($1 \le n \le 1000$), indicating the number of weights and holes. The next $n$ lines each contain $3$ integers $x_i, y_i, w_i$, denoting the coordinates of the $i$-th hole and the weight of the $i$-th object, respectively ($-10000 \le x_i, y_i \le 10000, 0 < w_i \le 1000$).

Your program must output two floating-point numbers (rounded to three decimal places), representing the $x$-coordinate and $y$-coordinate of the knot $x$ at the final equilibrium position. The two numbers are separated by a space.

The testdata guarantees that the balance point is unique, i.e., cases like $n=2$ with two equal masses will not appear. Translated by ChatGPT 5