P13380 [GCJ 2011 #3] Perpetual Motion

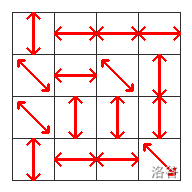
你去过 Google Lemming 工厂吗？那是一个非常特别的地方。地板被划分成 $R \times C$ 的网格。在每个网格单元内，都有一条传送带，方向可能是上下、左右，或者沿着两条对角线之一。每条传送带可以沿其方向前进或后退，你可以独立地为每条传送带选择这两种可能的移动方向之一。  现在，每个格子的中心都有一只旅鼠。当你启动传送带时，每只旅鼠会按照所在传送带的方向移动，直到到达新格子的中心。所有旅鼠会同时移动，这一过程恰好耗时 1 秒。之后，所有旅鼠都到达了新的格子中心，接下来会从新位置重复这一过程。这个过程会一直持续下去，除非你关闭传送带。 - 当一只旅鼠进入一个新格子时，它会继续沿原来的方向前进，直到到达该格子的中心。在下一秒开始前，它不会受到新传送带的影响。 - 如果一只旅鼠从网格边缘移动出去，它会从对面相同的位置回到网格。例如，如果它从左上角格子沿对角线向上左移动，它会到达右下角格子。科学的奇迹让这一切依然只需 1 秒完成。 - 旅鼠们永远不会相撞，也总能顺利穿过彼此。 关键在于为每条传送带选择方向，使得旅鼠们能够永远移动下去，且不会有两只旅鼠在同一时刻到达同一个格子中心。如果发生这种情况，它们就会粘在一起，从此无法分开，这对它们来说可不有趣。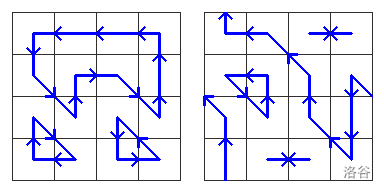 下面是之前示例中为每条传送带分配方向的两种方式：  在这两种情况下，都避免了两只旅鼠同时到达同一个格子中心。 给定任意的地板布局，请计算 $N$，即为每条传送带选择方向，使得不会有两只旅鼠同时到达同一个格子中心的方案数。由于答案可能很大，请输出 $N$ 对 $1000003$ 取模的结果。

输入的第一行为测试用例数 $T$。接下来有 $T$ 组测试数据。每组测试数据的第一行为两个正整数 $R$ 和 $C$。 接下来有 $R$ 行，每行包含一个长度为 $C$ 的字符串，字符串中的每个字符为 "|-/\\" 之一，表示该格子的传送带方向： - '|' 表示传送带可以向上或向下移动。 - '-' 表示传送带可以向左或向右移动。 - '/' 表示传送带可以向右上或左下移动。 - '\\' 表示传送带可以向左上或右下移动。

对于每组测试数据，输出一行，格式为 "Case #$x$: $M$"，其中 $x$ 为测试编号（从 1 开始），$M$ 为 $N$ 对 $1000003$ 取模的结果。

**数据范围** - $1 \leq T \leq 25$。 **小数据集（5 分，测试点 1 - 可见）** - $3 \leq R \leq 4$。 - $3 \leq C \leq 4$。 - 时间限制：3 秒。 **大数据集（21 分，测试点 2 - 隐藏）** - $3 \leq R \leq 100$。 - $3 \leq C \leq 100$。 - 时间限制：6 秒。 由 ChatGPT 4.1 翻译