P13398 [GCJ 2010 #1C] Making Chess Boards
Description
The chess board industry has fallen on hard times and needs your help. It is a little-known fact that chess boards are made from the bark of the extremely rare Croatian Chess Board tree, (Biggus Mobydiccus). The bark of that tree is stripped and unwrapped into a huge rectangular sheet of chess board material. The rectangle is a grid of black and white squares.
Your task is to make as many large square chess boards as possible. A chess board is a piece of the bark that is a square, with sides parallel to the sides of the bark rectangle, with cells colored in the pattern of a chess board (no two cells of the same color can share an edge).
Each time you cut out a chess board, you must choose the largest possible chess board left in the sheet. If there are several such boards, pick the topmost one. If there is still a tie, pick the leftmost one. Continue cutting out chess boards until there is no bark left. You may need to go as far as cutting out 1-by-1 mini chess boards.
Here is an example showing the bark of a Chess Board tree and the first few chess boards that will be cut out of it.
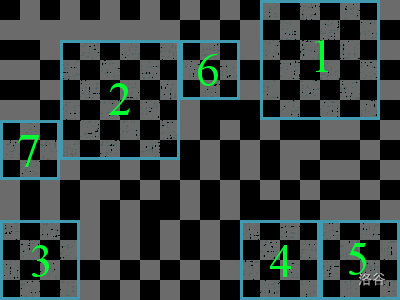
Input Format
The first line of the input gives the number of test cases, $T$. $T$ test cases follow. Each one starts with a line containing the dimensions of the bark grid, $M$ and $N$. $N$ will always be a multiple of $4$. The next $M$ lines will each contain an $(N/4)$-character hexadecimal integer, representing a row of the bark grid. The binary representation of these integers will give you a strings of $N$ bits, one for each row. Zeros represent black squares; ones represent white squares of the grid. The rows are given in the input from top to bottom. In each row, the most-significant bit of the hexadecimal integer corresponds to the leftmost cell in that row.
Output Format
For each test case, output one line containing "Case #$x$: $K$", where $x$ is the case number (starting from $1$) and $K$ is the number of different chess board sizes that you can cut out by following the procedure described above. The next $K$ lines should contain two integers each -- the size of the chess board (from largest to smallest) and the number of chess boards of that size that you can cut out.
Explanation/Hint
**Sample Explanation**
The first example test case represents the image above.
**Limits**
- $1 \leq T \leq 100$;
- $N$ will be divisible by 4;
- Each hexadecimal integer will contain exactly $N/4$ characters.
- Only the characters 0-9 and A-F will be used.
**Small dataset (18 Pts, Test set 1 - Visible)**
- $1 \leq M \leq 32$;
- $1 \leq N \leq 32$.
**Large dataset (24 Pts, Test set 2 - Hidden)**
- $1 \leq M \leq 512$;
- $1 \leq N \leq 512$;
- The input file will be at most 200kB in size.