P13400 [GCJ 2010 #2] World Cup 2010

四年一度的世界杯又来了，Varva 正赶往南非，正好赶上淘汰赛阶段。 在淘汰赛阶段，每场比赛必定有一个胜者；获胜的队伍晋级下一轮，失败的队伍则被淘汰。共有 $2^P$ 支队伍参加本阶段比赛，编号为 $0$ 到 $2^P - 1$。淘汰赛共进行 $P$ 轮。每一轮中，每支剩余的队伍都恰好参加一场比赛。每轮的对阵顺序是：依次选择剩余队伍中编号最小的两支队伍，将它们配对进行比赛。每一轮所有比赛结束后，下一轮开始。  为了决定看哪些比赛，Varva 根据自己对各支队伍的喜好，列出了一些限制条件。具体来说，对于每支队伍 $i$，他最多愿意错过 $M[i]$ 场该队参加的比赛。 Varva 需要提前购买一组门票，以确保无论比赛结果如何，他的偏好都能被满足。同时，他希望花的钱尽可能少。你的目标是计算他至少需要花多少钱买门票。 门票需要在比赛开始前提前购买，每场比赛的门票价格已知。注意，在小数据中，所有比赛的门票价格相同；而在大数据中，价格可能不同。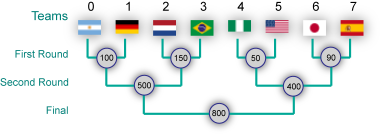 ### 示例 上图给出了一个比赛日程及门票价格。假设限制条件为 $M = \{1, 2, 3, 2, 1, 0, 1, 2, 3\}$，最优策略如下：由于不能错过队伍 $5$ 的任何比赛，需要花 $50, 400, 800$ 买下队伍 $5$ 可能参加的所有比赛门票。此时，其他队伍的限制也都被满足，除了队伍 $0$。为满足队伍 $0$ 的限制，最好的办法是再买下队伍 $0$ 第一轮比赛的门票，需再花 $100$，总共花费 $1350$。

输入的第一行为测试用例数 $T$。接下来是 $T$ 组测试数据。每组测试数据第一行为一个整数 $P$。下一行为 $2^P$ 个整数，分别为 $M[0], ..., M[2^P-1]$。 接下来的 $P$ 行给出了所有比赛的门票价格：第一行为第一轮的 $2^{P-1}$ 个比赛门票价格，第二行为第二轮的 $2^{P-2}$ 个比赛门票价格，依此类推。最后一行为决赛的门票价格。门票价格按照比赛进行的顺序给出。

对于每个测试用例，输出一行，格式为 "Case #x: y"，其中 $x$ 为测试用例编号（从 1 开始），$y$ 为 Varva 至少需要花费的门票总金额。

**数据范围** - $1 \leq T \leq 50$ - $1 \leq P \leq 10$ - $M$ 中每个元素为 $0$ 到 $P$ 之间的整数（包含 $0$ 和 $P$） **小数据（10 分，测试点 1 - 可见）** - 所有门票价格均为 1。 **大数据（15 分，测试点 2 - 隐藏）** - 所有门票价格为 $0$ 到 $100000$ 之间的整数（包含 $0$ 和 $100000$）。 由 ChatGPT 4.1 翻译