P13402 [GCJ 2010 #2] Grazing Google Goats

约翰农夫最近为他的牧场添置了一群 $N$ 只山羊。每只山羊 $i$ 将被用一根长度为 $L_i$ 的绳子拴在某个位置 $P_i$ 的木桩上。这意味着山羊可以在距离 $P_i$ 不超过 $L_i$ 的范围内自由活动，但不能到达其他地方。（牧场很大且平坦，可以看作是一个无限的二维平面。） 约翰农夫已经选好了木桩的位置，这些位置是他上一次养山羊时留下的，但他还需要决定每根绳子的长度。这个决定有两个难点： - 所有山羊都必须能够到达同一个水桶。约翰农夫还没有决定水桶的具体位置。他已经将选择范围缩小到一组位置 $\{Q_1, Q_2, \ldots, Q_M\}$，但还不确定最终选哪个。 - 山羊们脾气暴躁，聚在一起时有时会吵闹打架。为了大家的安宁，约翰农夫希望最小化所有山羊都能到达的区域面积 $A$。 不幸的是，约翰农夫不擅长几何学，他需要你来帮忙解决这个问题！ 对于每个水桶位置 $Q_j$，你需要选择合适的绳子长度，使得当水桶放在 $Q_j$ 时，所有山羊都能到达水桶，并且所有山羊都能到达的区域面积 $A_j$ 最小。你需要计算出每个 $A_j$。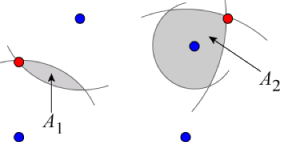 ### 示例 下图中有四个蓝点，分别对应木桩位置 $P_1$、$P_2$、$P_3$ 和 $P_4$。还有两个红点，分别对应可能的水桶位置 $Q_1$ 和 $Q_2$。你需要计算 $A_1$ 和 $A_2$，即两块阴影区域的面积。 

第一行输入测试用例数 $T$。接下来有 $T$ 组测试数据。每组测试数据第一行包含两个整数 $N$ 和 $M$。 接下来的 $N$ 行，每行给出一个木桩位置 $P_1, P_2, \ldots, P_N$。之后的 $M$ 行，每行给出一个水桶位置 $Q_1, Q_2, \ldots, Q_M$。 每个位置的坐标均为一行，包含该点的 $x$ 和 $y$ 坐标，用一个空格分隔。

对于每组测试数据，输出一行，格式为 “Case #$x$: $A_1$ $A_2$ ... $A_M$”，其中 $x$ 为测试用例编号（从 1 开始），$A_1$ $A_2$ ... $A_M$ 分别为上述定义的面积。只要答案的相对或绝对误差不超过 $10^{-6}$，即视为正确。

**数据范围** - 所有坐标均为 $-10,000$ 到 $10,000$ 之间的整数。 - 所有 $P_1, P_2, \ldots, P_N, Q_1, Q_2, \ldots, Q_M$ 位置均互不相同，且任意三点不共线。 **小数据（7 分，测试点 1 - 可见）** - 时间限制：~~30~~ 3 秒。 - $1 \leq T \leq 100$。 - $N = 2$。 - $1 \leq M \leq 10$。 **大数据（25 分，测试点 2 - 隐藏）** - 时间限制：~~120~~ 12 秒。 - $1 \leq T \leq 10$。 - $2 \leq N \leq 5,000$。 - $1 \leq M \leq 1,000$。 由 ChatGPT 4.1 翻译