P13407 [GCJ 2010 Finals] Letter Stamper

Roland 是一名高中数学老师。每天，他都会收到学生们交上来的上百份试卷。对于每份试卷，他都会仔细地选择一个字母成绩：'A'、'B' 或 'C'。（Roland 的学生都很聪明，不会拿到 'D' 或 'F' 这样的低分。）一旦所有成绩都确定后，Roland 会把试卷交给他的助理——你。你的任务是把正确的成绩盖在每份试卷上。 你有一个低科技但实用的字母印章。要打印一个字母，你需要将对应字母的专用印版装到印章前端，蘸上墨水，然后盖在试卷上。 有趣的是，当你想要切换字母时，无需取下原来的印版，你只需把新的印版直接叠加在旧的印版上。实际上，你可以把印章上的印版看作一个栈，支持以下操作： - 将一个字母压入栈顶（即把新的印版装到印章前端）。 - 从栈顶弹出一个字母（即把印章前端的印版取下）。 - 打印栈顶的字母（即实际盖章）。当然，栈中必须有印版才能进行此操作。 给定一个字母成绩序列（只包含 'A'、'B' 和 'C'），你需要用最少的操作数按顺序打印出整个序列。初始时栈为空，结束时你也必须将栈清空。在操作过程中，你有无限数量的每种印版可用。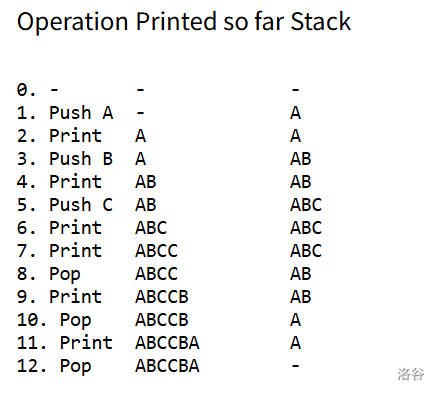 例如，如果你要打印序列 "ABCCBA"，你可以用 12 次操作完成，如下图所示： 

输入文件的第一行包含测试用例数 $T$。接下来的 $T$ 行，每行包含一个字符串 $S$，表示你要按顺序打印的字母序列。

对于每个测试用例，输出一行，格式为 "Case #$x$: $N$"，其中 $x$ 是测试用例编号（从 1 开始），$N$ 是打印出 $S$ 所需的最少栈操作数。

**限制条件** - $S$ 是一个非空字符串，只包含字母 'A'、'B' 和 'C'。 **小数据集（8 分，测试集 1 - 可见）** - $1 \leq T \leq 100$。 - $S$ 最多包含 $100$ 个字符。 **大数据集（19 分，测试集 2 - 隐藏）** - $1 \leq T \leq 20$。 - $S$ 最多包含 $7000$ 个字符。 由 ChatGPT 4.1 翻译