P13411 [GCJ 2010 Finals] Ninjutsu

忍术是神秘的日本刺客——忍者——的武术。作为忍术初学者，你的第一个任务是掌握抓钩的使用。 抓钩是一种技术先进的装置，由一根（非常坚固且非常细的）绳子系着一个钩子组成。正确使用抓钩的方法是将钩子投向目标，并希望它能够勾住目标。 这一次，你成功了！你现在已经勾住了位于 $(0, 0)$ 的目标。你的绳子向左延伸，你正处于绳子的末端；当你跳起时，你会开始围绕目标逆时针摆动。还有其他目标位于 $(0, 0)$ 的右侧和上方，坐标为 $(x_i, y_i)$，其中 $x_i \geq 0$ 且 $y_i \geq 0$。当绳子的内部某一点（不是两端）接触到一个或多个目标时，绳子会围绕距离其运动端最近的目标弯折。忽略你的初始速度；因为你是忍者，你的速度足够快，你会不断围绕目标弯折，直到你只围绕一个目标旋转。 你当前的绳子长度为 $R$，但你可以选择在开始摆动前将其剪短为任意更短的长度 $r$（包括非整数长度）。因此，你将从 $(-r, 0)$ 出发，向下（逆时针）摆动至 $(0, -r)$。 你能在一次摆动中让绳子最多弯折多少次？每当你的绳子触碰到一个目标，并且随后围绕该目标旋转了非零角度时，就算作一次弯折。绳子始终保持完全笔直（这同样是因为你是忍者），除了在弯折处。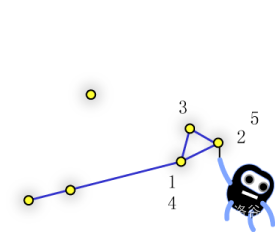 ### 示例  在上面的例子中，有 6 个点： - $(0, 0)$， - $(3, 1)$， - $(12, 4)$， - $(14, 5)$， - $(13, 7)$， - $(7, 10)$。 你有一根长度为 $24$ 的绳子。如果你不剪短绳子，那么你会依次围绕点 $(12, 4)$、$(14, 5)$、$(13, 7)$ 弯折，最后会被困在点 $(7, 10)$ 附近旋转，剩余绳长约为 $0.1705$。这样总共发生了 $4$ 次弯折。虽然你会触碰到点 $(3, 1)$，但由于它与点 $(0, 0)$ 和 $(12, 4)$ 共线，因此不算作一次弯折。 然而，如果你将绳子剪短 $0.18$ 个单位长度，你将无法到达点 $(7, 10)$，而是会按照以下路径移动： $(0, 0)$--$(12, 4)$--$(14, 5)$--$(13, 7)$--$(12, 4)$--$(14, 5)$ 最终会在点 $(14, 5)$ 附近旋转，剩余绳长约为 $1.3004$。这个路径总共发生了 $5$ 次弯折，是最优解。  下面的样例输入中的第 1 组数据对应上述例子。

输入的第一行为一个整数 $T$，表示接下来的测试用例数量。每组测试用例的第一行为两个整数 $N$ 和 $R$。接下来的 $N$ 行，每行包含一对整数 $x_i$ 和 $y_i$，表示目标的坐标，第一组坐标为 $(0, 0)$。

对于每组测试用例，输出一行，格式为 "Case #$C$: $k$"，其中 $C$ 为测试用例编号（从 1 开始），$k$ 为一次摆动中最多能发生的弯折次数。

**数据范围** - $1 \leq T \leq 100$ - 所有目标坐标均为整数。 - 所有目标位置均不相同。 - 第一组目标坐标为 $(0, 0)$。 - 至少存在一个 $r$，使得以长度 $r - 0.999999$ 的绳子也能得到最优解（即弯折序列相同）。 **小数据（11 分，测试点 1 - 可见）** - $1 \leq N \leq 10$ - $1 \leq R \leq 1,000$ - $0 \leq x_i \leq 1,000$ - $0 \leq y_i \leq 1,000$ **大数据（23 分，测试点 2 - 隐藏）** - $1 \leq N \leq 1,000$ - $1 \leq R \leq 10^9$ - $0 \leq x_i \leq 10^9$ - $0 \leq y_i \leq 10^9$ 由 ChatGPT 4.1 翻译