P13412 [GCJ 2010 Finals] The Paths of Yin Yang

> 故有无相生， > 难易相成， > 长短相形， > 高下相倾， > 音声相和， > 前后相随。 > ——《道德经》老子，周朝，中国古代

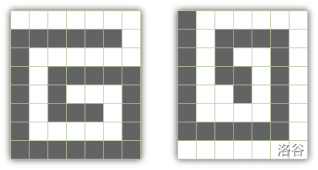
给定一个 $N$ 行 $M$ 列的矩形网格，每个格子可以标记为黑色（阴）或白色（阳）。如果两个格子共享一条单位长度的边，则它们是相邻的。如果所有黑色格子构成一条路径，且所有白色格子也构成一条路径，则称该网格是合法的。路径是指满足以下条件的格子集合 $s$： - 这些格子连成一块。从 $s$ 中的任意一个格子出发，只通过 $s$ 内的相邻格子可以到达 $s$ 中的任意一个格子。 - 恰好有两个格子在 $s$ 中只有一个相邻格子（即“端点”）。 - $s$ 中的其他每个格子都有恰好两个相邻格子。 例如，下图中，第一个网格是合法的，而第二个网格不是——虽然黑色格子构成了一条路径，但白色格子没有。  给定 $N$ 和 $M$，计算合法网格的数量。注意，对称性不影响结果——只要两个合法网格在某个位置不同，即使一个可以通过旋转或翻转变为另一个，也认为它们是不同的。

输入的第一行为一个整数 $T$，表示测试用例的数量。接下来的 $T$ 行，每行包含两个用空格分隔的整数：“$N$ $M$”，如上所述。

对于每个测试用例，输出一行，格式为 “Case #$x$: $A$”，其中 $x$ 是测试用例编号（从 1 开始），$A$ 是指定大小网格的合法方案数。

**数据范围** - $1 \leq T \leq 50$ **小数据集（测试集 1 - 可见）** - 时间限制：~~30~~ 15 秒每组数据。 - $4 \leq N, M \leq 10$ **大数据集（测试集 2 - 隐藏）** - 时间限制：~~120~~ 60 秒每组数据。 - 对于 80% 的测试用例，$4 \leq N, M \leq 50$ - 对于 90% 的测试用例，$4 \leq N, M \leq 70$ - 对于所有测试用例，$4 \leq N, M \leq 100$ 由 ChatGPT 4.1 翻译