P13412 [GCJ 2010 Finals] The Paths of Yin Yang

> So, If and Else grow out of each other; > Hardness and Tractability complete each other; > Long int and Short int shape each other; > High bits and Low bits determine each other; > Music and Voice give harmony to each other; > Push_front and Push_back give sequence to each other. -- Tao Te Ching, Laozi, Zhou dynasty, ancient China. Translated (loosely) by yours truly.

Given an rectangular grid of $N$ rows and $M$ columns, each cell can be labeled black (Yin) or white (Yang). Two cells are neighbors if they share a common unit-length edge segment. The grid is valid if all the black cells form a path, and all the white cells form a path. A path is a set $s$ of cells defined as follows: * The cells form a connected piece. From each cell in $s$, you can reach any other cell in $s$ by moving between neighbors within $s$. * Exactly two cells in $s$ have exactly one neighbor in $s$ each. These are the "ends" of the path. * Every other cell in $s$ has exactly two neighbors in $s$. For example, in the picture below, the first grid is valid, while the second grid is not -- although the black cells form a path, the white cells do not.  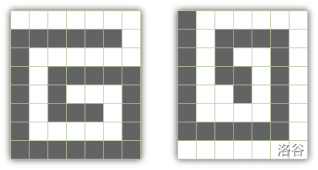Given $N$ and $M$, compute the number of valid grids. Note that symmetry doesn't matter -- as long as two valid grids differ in one position they are considered different, even if one can be rotated or flipped to the other.

The first line of the input will be a single integer $T$, the number of test cases. $T$ lines follow, each of which contains two integers separated by a space: "$N$ $M$", as defined above.

For each test case, output a line in the form "Case #$x$: $A$", where $x$ is the case number, starting from 1, and $A$ is the number of valid grids of the specified size.

**Limits** - $1 \leq T \leq 50$ **Small dataset (Test set 1 - Visible)** - Time limit: ~~30~~ 15 seconds per test set. - $4 \leq N, M \leq 10$ **Large dataset (Test set 2 - Hidden)** - Time limit: ~~120~~ 60 seconds per test set. - For 80% of the test cases, $4 \leq N, M \leq 50$ - For 90% of the test cases, $4 \leq N, M \leq 70$ - For all test cases, $4 \leq N, M \leq 100$