P13418 [COCI 2012/2013 #4] AKVARIJ

Mirko 最近安装了一个新的屏保。如果他离开键盘五分钟，屏幕上就会显示一幅有动画鱼的水族箱图片。这个屏保可以自定义（虚拟的、带沙底的）水族箱底部的形状以及水位高度。 这个水族箱可以用二维直角坐标系来表示，宽度为 $N-1$ 列，其中 $N$ 是正整数。水族箱的左侧壁的 $x$ 坐标为 $0$，右侧壁的 $x$ 坐标为 $N-1$。水族箱底部每一个整数 $x$ 坐标（记为 $i$，$0 \leq i \leq N-1$）都有一个可以单独调整的高度 $H_i$。对于任意相邻的整数坐标 $i$ 和 $i+1$，底部由 $(i, H_i)$ 到 $(i+1, H_{i+1})$ 的线段描述。 如果水位设为 $h$，水会填满 $y = h$ 与水族箱底部之间的区域。若某些底部高于水位 $h$，则这些部分会形成“岛屿”，不会被水淹没。 对于不同的水族箱底部形状，Mirko 想知道屏幕上被水覆盖的总面积。请帮 Mirko 解答这个问题（除了 42 以外的答案）。

第一行输入两个正整数 $N$（$3 \leq N \leq 100\,000$，底部长度）和 $M$（$1 \leq M \leq 100\,000$，询问数量）。 第二行输入 $N$ 个非负整数 $H_i$（$0 \leq H_i \leq 1000$），表示初始底部的高度。 接下来的 $M$ 行，每行一个询问，格式如下两种之一： - Q $h$ —— 若水位为 $h$（$0 \leq h \leq 1000$），在当前底部形状下，被水覆盖的总面积是多少？ - U $i$ $h$ —— Mirko 决定将 $x$ 坐标为 $i$（$0 \leq i \leq N-1$）处的底部高度改为 $h$（$0 \leq h \leq 1000$），即 $H_i = h$。

对于每个 Q 类型的询问，输出一行，表示所求面积，四舍五入保留三位小数。答案与官方标准答案的误差不超过 $0.001$ 即可。

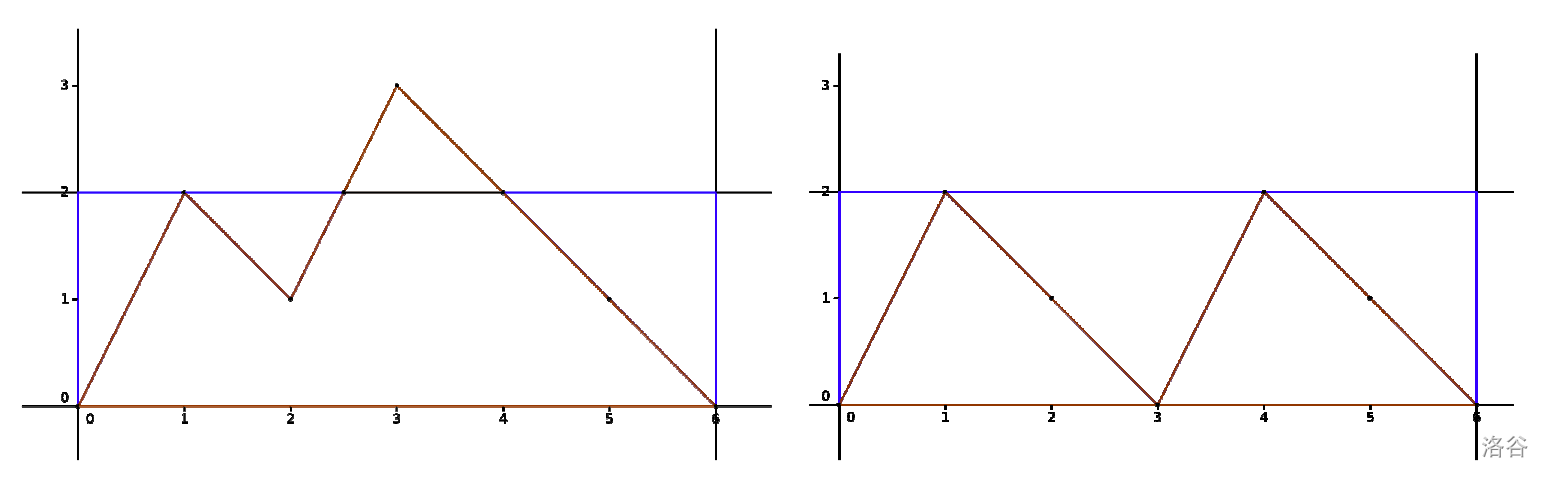
第三个样例的说明：下图左侧是修改前，右侧是 U 类型操作后，水位 $h=2$（Q 2 询问）的情形。左图淹没面积为 $3.75$，右图为 $6$。  翻译由 ChatGPT-4.1 完成。