P13427 [COCI 2020/2021 #2] Odasiljaci

遗憾的是，这将是 Sean 最后一次扮演 James Bond。 他的任务是在一片广阔的沙漠中组网 $n$ 个分散的天线。这片沙漠可以看作一个二维平面。Sean 会将每个天线的发射半径都设置为同一个非负实数 $r$。天线的覆盖范围被定义为：到该天线的距离不超过 $r$ 的所有点的集合。如果两个天线的覆盖范围有公共点，则这两个天线可以直接通信。此外，如果天线 $A$ 能与 $B$ 通信，$B$ 能与 $C$ 通信，那么 $A$ 也可以通过 $B$ 与 $C$ 通信。 Sean 想要让所有天线连成一个网络，即使任意两个天线都可以通信。由于 $M$ 限制了他的花费，而更大的半径意味着更高的成本，Sean 会选择尽可能小的半径 $r$。请你帮他解决这个问题！

第一行输入一个整数 $n$（$1 \leq n \leq 1000$），表示天线的数量。 接下来的 $n$ 行，每行输入两个整数 $x_i$ 和 $y_i$（$0 \leq x_i, y_i \leq 10^9$），表示第 $i$ 个天线的坐标。

输出最小所需半径 $r$。 只要你的答案的绝对误差或相对误差不超过 $10^{-6}$，就会被视为正确。

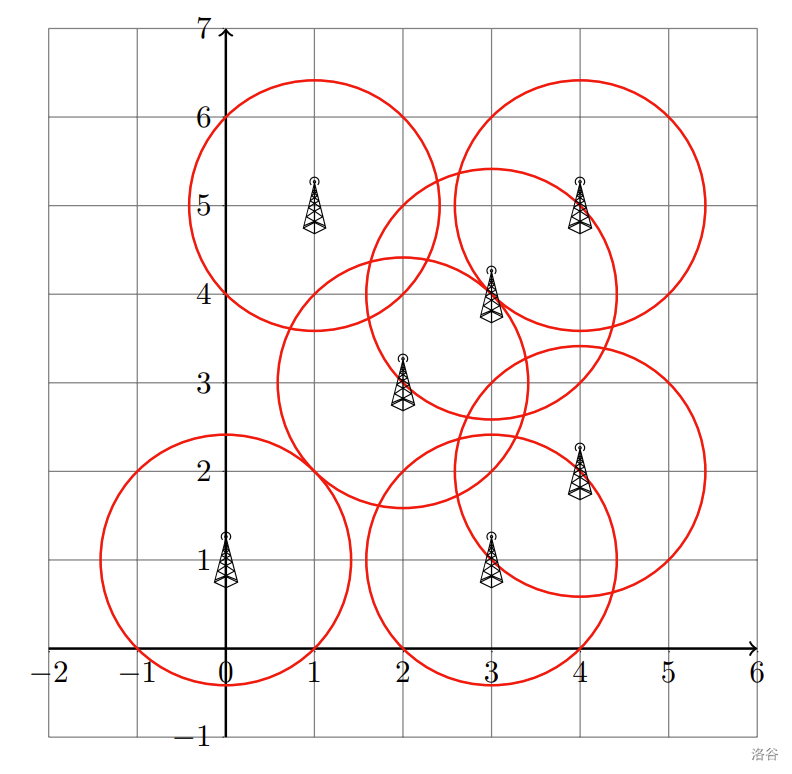
第二个样例的示意图如下：  翻译由 ChatGPT-4.1 完成。