P13427 [COCI 2020/2021 #2] Odasiljaci

Sadly, this is the last time Sean will play James Bond. His mission is to network $n$ antennas that are scattered across a vast desert, which can be represented as a 2D plane. He will set the transmission radius of each antenna to be the same non negative real number $r$. The range of an antenna is defined as the set of all points whose distance to the antenna is at most $r$. If ranges of two antennas have a common point, those antennas can directly communicate. Also, if antennas $A$ and $B$ can communicate, as well as antennas $B$ and $C$, then antennas $A$ and $C$ are also able to communicate, through antenna $B$. Sean wants to network the antennas, i.e. make possible for every two antennas to communicate. Since $M$ has limited his spending for this mission, and larger radii require more money, Sean will choose the smallest possible radius $r$. Help him solve this problem!

The first line contains an integer $n$ ($1 \leq n \leq 1000$), the number of antennas. Each of the following $n$ lines contains integers $x_i$ and $y_i$ ($0 \leq x_i, y_i \leq 10^9$), coordinates of the $i$-th antenna.

Output the minimal radius. Your answer will be considered correct if its absolute or relative error doesn't exceed $10^{-6}$.

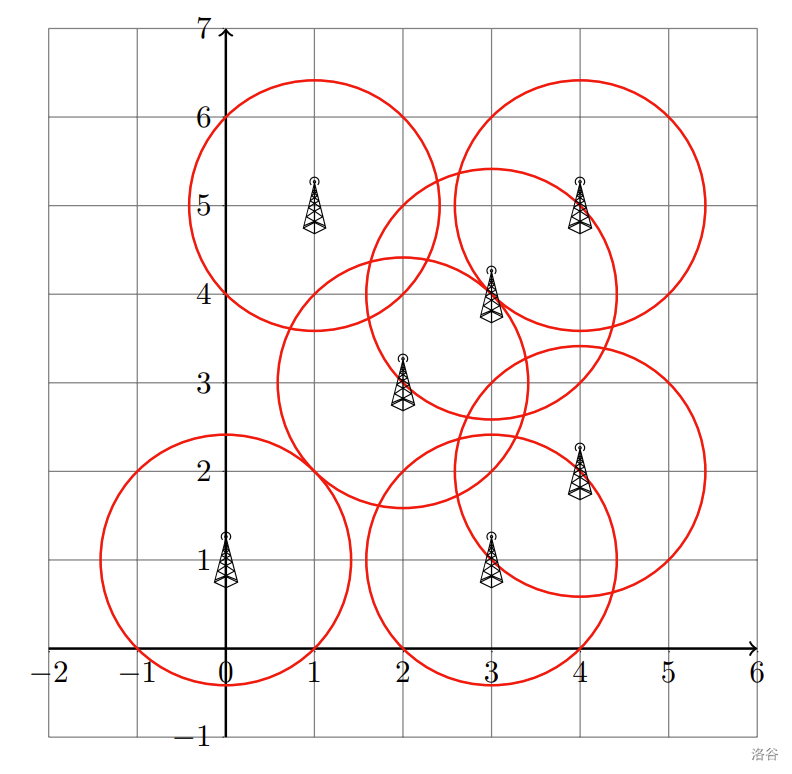
Clarification of the second example: