P13466 [GCJ 2008 #2] Cheating a Boolean Tree
题目描述
在本题中,我们将考虑一种称为布尔树的二叉树。在这种树中,除了最后(最深)一层外,每一层都被完全填满,并且最后一层的节点尽可能靠左。此外,树中的每个节点要么有 $0$ 个子节点,要么有 $2$ 个子节点。
布尔树的特殊之处在于,每个节点都与一个布尔值相关联,取 $1$ 或 $0$。此外,每个内部节点都与一个“AND”或“OR”门相关联。一个“AND”门节点的值由其两个子节点的值进行逻辑与运算得到。同理,“OR”门节点的值由其两个子节点的值进行逻辑或运算得到。所有叶子节点的值将作为输入给出,因此可以自底向上计算所有节点的值。
我们特别关注树的根节点。我们希望根节点的值为 $V$,即 $1$ 或 $0$。不幸的是,根节点的实际值可能并非如此。幸运的是,我们可以作弊,将某些节点的门类型进行更改;即可以将 AND 门改为 OR 门,或将 OR 门改为 AND 门。
给定一个布尔树的描述以及哪些门可以更改,求最少需要更改多少个门,才能使根节点的值为 $V$。如果无法实现,则输出 "IMPOSSIBLE"(带引号,仅为清晰起见)。
输入格式
输入的第一行包含测试用例数 $N$。接下来有 $N$ 个测试用例。
每个测试用例以 $M$ 和 $V$ 开头。$M$ 表示树中节点的数量,且 $M$ 为奇数,以确保所有节点要么有 $0$ 个子节点,要么有 $2$ 个子节点。$V$ 是根节点期望的值,取 $0$ 或 $1$。
接下来的 $M$ 行描述树中每个节点。第 $X$ 行描述编号为 $X$ 的节点,节点编号从 $1$ 开始。
前 $(M-1)/2$ 行描述内部节点。每行包含 $G$ 和 $C$,均为 $0$ 或 $1$。若 $G$ 为 $1$,则该节点为 AND 门,否则为 OR 门。若 $C$ 为 $1$,则该门类型可以更改,否则不可更改。内部节点 $X$ 的两个子节点分别为 $2X$ 和 $2X+1$。
接下来的 $(M+1)/2$ 行描述叶子节点。每行包含一个值 $I$,为 $0$ 或 $1$,表示该叶子节点的值。
为帮助理解,以下是第一个样例输入对应的树结构图:
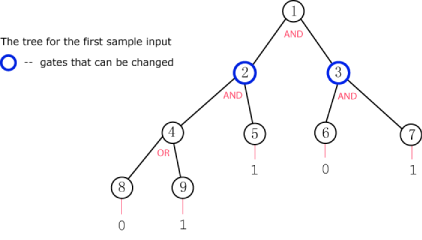
输出格式
对于每个测试用例,输出:
Case #X: Y
其中 $X$ 是测试用例编号,$Y$ 是使根节点输出为 $V$ 所需更改门的最小次数;如果无法实现,则输出 "IMPOSSIBLE"(带引号,仅为清晰起见)。
说明/提示
**样例说明**
在第 1 个测试用例中,我们可以将节点 3 的门更改为 OR 门,从而使根节点达到期望的结果。
在第 2 个测试用例中,只有根节点可以更改,但将其改为 OR 门也无法实现目标。
**数据范围**
- $1 < N \leq 20$
**小数据集(5 分,测试点 1 - 可见)**
- $2 < M < 30$
**大数据集(10 分,测试点 2 - 隐藏)**
- $2 < M < 10000$
由 ChatGPT 4.1 翻译