P13502 [OOI 2024] Draw Polygon Lines

*This is an interactive problem.* You are given $n$ points $A_i = (x_i, y_i)$ on the plane. It is known that all $x_i$ are distinct and all $y_i$ are distinct. Your task is to draw polygonal lines connecting these $n$ points. A polygonal line is defined by a permutation $p_1, p_2, \ldots, p_n$ of numbers from $1$ to $n$. The polygonal line consists of $n-1$ segments, the first segment connects points $A_{p_1}$ and $A_{p_2}$, the second segment connects points $A_{p_2}$ and $A_{p_3}$, $\ldots$, the last segment connects points $A_{p_{n-1}}$ and $A_{p_n}$. Note that segments may intersect. The $\textit{sharpness}$ of a polygonal line is defined as the number of indices $2 \leq i \leq n - 1$ such that the angle $\angle A_{p_{i-1}} A_{p_i} A_{p_{i+1}}$ is acute, i.e., strictly less than $90^{\circ}$. You need to solve four tasks: - Find any polygonal line that has the maximum possible sharpness. - Given an integer $c$. Find any polygonal line whose sharpness is $\leq c$. - Given an integer $c$. Answer $q$ queries, each specified by a single integer $k_i$ ($c \leq k_i \leq n - c$). In the $i$-th query, you need to construct a polygonal line that has sharpness exactly $k_i$. - Given an integer $c$. For each $k$ from $c$ to $n - c$, construct a polygonal line $p^{(k)}$ with sharpness exactly $k$. Provide $n - 2c + 1$ numbers $\text{hash}\left(p^{(c)}\right), \text{hash}\left(p^{(c+1)}\right), \ldots, \text{hash}\left(p^{(n-c)}\right)$ as the answer, where $hash(p) = \left( \sum\limits_{i=1}^{n} p_i b^{i-1} \right) \bmod m$ is the polynomial hash of permutation $p$ with parameters $b = 10^6 + 3$ and $m = 10^9 + 7$. Then answer $q$ queries, each specified by a single integer $k_i$ ($c \leq k_i \leq n - c$). In the $i$-th query, you need to provide the polygonal line $p^{(k_i)}$. It will be checked that the sharpness of this polygonal line is exactly $k_i$ and its hash matches the previously provided value $\text{hash}\left(p^{(k_i)}\right)$. Note that queries will appear after receiving the hashes. It is guaranteed, that under given constraints, the answers always exist. ### Interaction Protocol The first line contains two integers $\text{task}$, $\text{group}$ ($1 \leq \text{task} \leq 4$, $0 \leq \text{group} \leq 21$) --- the number of the task to be solved in this test and the test group number. The second line contains a single integer $n$ ($3 \leq n \leq 80\,000$) --- the number of points on the plane. Each of the next $n$ lines contains two integers $x_i$, $y_i$ ($|x_i|, |y_i| \leq 10^9$) --- the coordinates of the points. It is guaranteed that all $x_i$ are distinct and all $y_i$ are distinct. If $\text{task} = 1$, then the input ends here and you should output any permutation with the maximum possible sharpness. The interaction ends here. If $\text{task} \neq 1$, then the next line contains a single integer $c$ ($2 \leq c \leq \frac{n}{2}$). If $\text{task} = 2$, then the input ends here and you should output any permutation with sharpness $\leq c$. The interaction ends here. If $\text{task} = 4$, your solution should output $n - 2c + 1$ integers $\text{hash}\left(p^{(c)}\right), \text{hash}\left(p^{(c+1)}\right), \ldots, \text{hash}\left(p^{(n-c)}\right)$, where $0 \leq \text{hash}\left(p^{(i)}\right) < 10^9 + 7$. Note that this should not be done if $\text{task} = 3$. Further interaction occurs only if $\text{task} = 3$ or $\text{task} = 4$. The next line contains a single integer $q$ ($1 \leq q \leq 50$) --- the number of queries. Then $q$ times, in each line, a query $k_i$ ($c \leq k_i \leq n - c$) appears. As a response, you should output a permutation on a separate line. The sharpness of this permutation should be exactly $k_i$. If $\text{task} = 4$, the hash of this permutation should match the previously provided hash. **Since this is an interactive problem, after outputting each line, do not forget to output a newline character and flush the output buffer.**

N/A

N/A

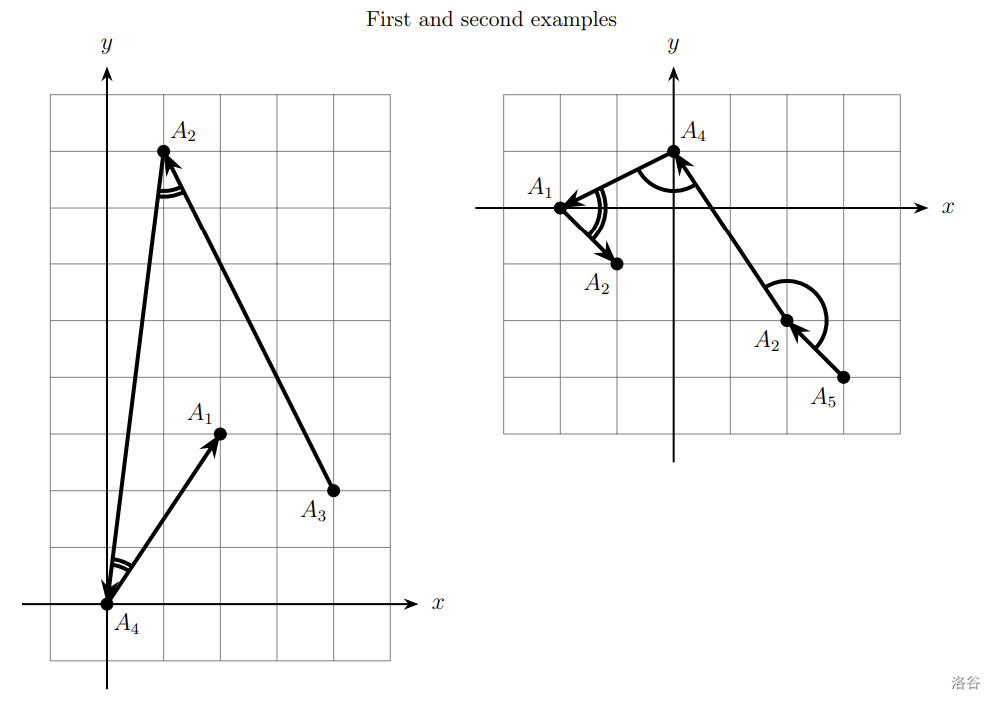
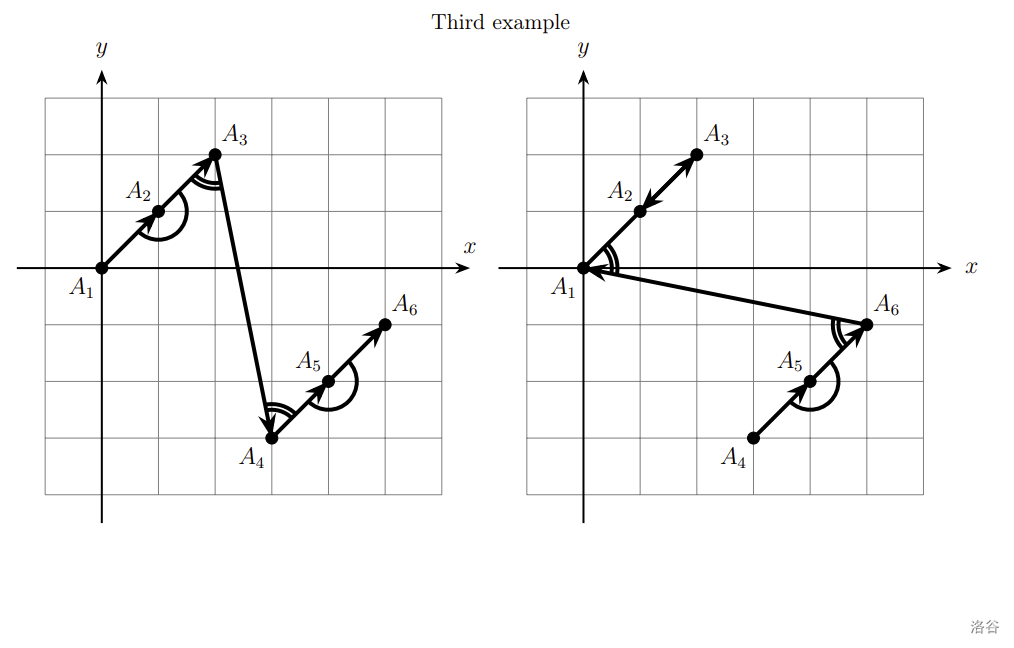
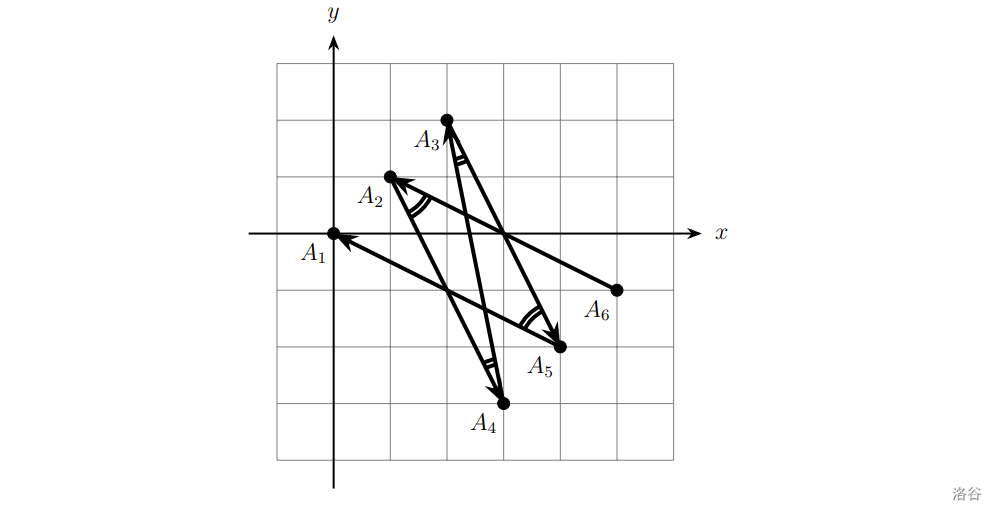
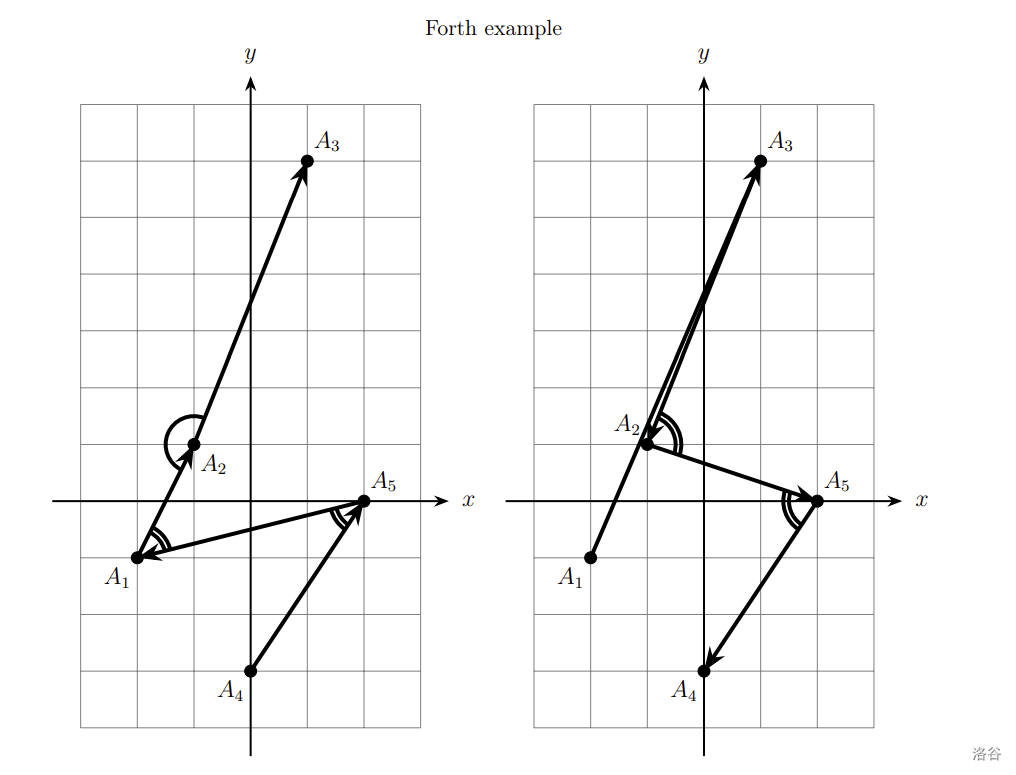
### Note In all the figures, acute angles are denoted by two arcs, and non-acute angles are denoted by a single arc.  In the first example all angles are sharp, so the line has maximum sharpness $2$. In the second sample the sharpness equals to $1$, it is $\leq 2$.   In the third example the lines have sharpness $2$, $3$, $4$.  In the forth example we build lines that have sharpness $2$ and $3$. The lines have hashes equal to the ones provided earlier. ### Scoring The tests for this problem consist of twenty-one groups. Points for each group are given only if all tests of the group and all tests of the required groups are passed. | Group | Points | task | $n$ | $c$ | Additional constraints | Required Groups | Comment | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 0 | 0 | - | - | - | - | - | Examples. | | 1 | 8 | 1 | $n \leq 20000$ | - | $x_i < x_{i+1}, y_i < y_{i+1}$ | - | | | 2 | 6 | 1 | $n \leq 10$ | - | random points | - | | | 3 | 5 | 1 | $n \leq 1000$ | - | random points | 2 | | | 4 | 5 | 1 | $n \leq 20000$ | - | random points | 2 - 3 | | | 5 | 6 | 1 | $n \leq 20000$ | - | - | 1 - 4 | | | 6 | 17 | 2 | $n = 80000$ | $c = 800$ | - | - | | | 7 | 7 | 3 | $n = 80000$ | $c = 800$ | $x_i < x_{i+1}, y_i < y_{i+1}$ | - | | | 8 | 4 | 3 | $n = 50$ | $c = 25$ | random points | - | | | 9 | 4 | 3 | $n = 200$ | $c = 80$ | random points | - | | | 10 | 4 | 3 | $n = 1000$ | $c = 300$ | random points | - | | | 11 | 3 | 3 | $n = 5000$ | $c = 600$ | random points | - | | | 12 | 3 | 3 | $n = 80000$ | $c = 35000$ | random points | - | | | 13 | 3 | 3 | $n = 80000$ | $c = 5000$ | random points | 12 | | | 14 | 3 | 3 | $n = 80000$ | $c = 2000$ | - | 12 - 13 | | | 15 | 2 | 3 | $n = 80000$ | $c = 800$ | - | 7, 12 - 14 | | | 16 | 6 | 4 | $n = 80000$ | $c = 800$ | $x_i < x_{i+1}, y_i < y_{i+1}$ | - | | | 17 | 3 | 4 | $n = 5000$ | $c = 600$ | random points | - | | | 18 | 3 | 4 | $n = 80000$ | $c = 35000$ | random points | - | | | 19 | 3 | 4 | $n = 80000$ | $c = 5000$ | random points | 18 | | | 20 | 3 | 4 | $n = 80000$ | $c = 2000$ | - | 18 - 19 | | | 21 | 2 | 4 | $n = 80000$ | $c = 800$ | - | 16, 18 - 20 | | In the groups where it is indicated that the points are random, all coordinates of all points $x_i$, $y_i$ are randomly generated with equal probability in the interval $[-10^9, 10^9]$.