P13503 [OOI 2024] Evidence Board

Volodya 梦想成为一名侦探。因此，Volodya 经常阅读讲述破案传奇的书籍。在研究下一个案件时，Volodya 发现了调查过程中的一些有趣细节。 本案共有 $n$ 名嫌疑人。证据板上包含了全部 $n$ 个人。最初，嫌疑人之间没有任何联系。 在调查过程中，嫌疑人之间逐渐出现了新的联系。每一条新联系都连接了此前尚未直接或间接（通过其他人）相连的两个人。 让我们来看一下当 $A$ 和 $B$ 之间出现一条联系时的情况。除了涉及的两个人名字外，每条联系还包含三个参数：$c_A$ —— 针对 $A$ 的证据强度，$c_B$ —— 针对 $B$ 的证据强度，$w_{AB}$ —— 这条联系的总证据强度。出于自然原因，联系的证据强度不能超过针对 $A$ 和 $B$ 的证据强度之和。也就是说，对于每一条联系，**一定**有 $w_{AB} \leq c_A + c_B$。侦探们在获得这样一条联系时，会在证据板上将 $A$ 和 $B$ 的照片之间画一条线，并将 $w_{AB}$ 标注在这条线上。同时，会在 $A$ 的照片上贴上写有 $c_A$ 的便签，在 $B$ 的照片上贴上写有 $c_B$ 的便签。如果照片上已经有其他便签，则新便签会贴在旧便签之上。 案件正是在所有嫌疑人通过 $n-1$ 条联系连通时被侦破的。破案后，证据板以原貌被陈列在博物馆中。 受到这种方式的启发，Volodya 参观了博物馆，并详细研究了这块证据板。Volodya 注意到，对于每个人 $v$，其照片上从上到下贴有编号为 $c_{v,1}, \ldots, c_{v,deg_v}$ 的便签。这里 $deg_v$ 表示与 $v$ 相关的联系数量。同时，Volodya 记得第 $i$ 条联系发生在 $a_i$ 和 $b_i$ 之间，证据强度为 $w_i$。不幸的是，这些联系的编号是随意的，并不一定与它们在调查中出现的先后顺序一致。 由于联系编号的混乱，证据板上的信息无法帮助还原调查过程。现在 Volodya 需要你帮助他还原一种可能的、侦探们获得这些联系的时间顺序。如果不存在符合条件的顺序，也有可能是博物馆伪造了信息。

输入的第一行包含两个整数 $n$ 和 $g$（$2 \le n \le 200\,000$，$0 \le g \le 9$），分别表示案件中的嫌疑人数和测试组编号。 接下来 $n-1$ 行描述每一条联系。第 $i$ 行包含三个整数 $a_i$、$b_i$、$w_i$（$1 \le a_i, b_i \le n$，$1 \le w_i \le 10^9$，$a_i \neq b_i$），表示第 $i$ 条联系连接了 $a_i$ 和 $b_i$，证据强度为 $w_i$。保证所有嫌疑人最终连通。 接下来 $n$ 行描述便签上的数字。第 $i$ 行包含 $deg_i$ 个整数 $c_{i, 1}, \ldots, c_{i, deg_i}$（$0 \le c_{i, j} \le 10^9$），表示第 $i$ 个人照片上从上到下的便签数字。$deg_i$ 等于与第 $i$ 个人相关的联系数量。

如果不存在符合条件的还原顺序，输出一行 `No`（不含引号）。 否则，第一行输出 `Yes`（不含引号）。第二行输出 $n-1$ 个数字，表示一种符合条件的联系出现顺序。联系编号为 $1$ 到 $n-1$，顺序与输入一致。如果存在多种可能的顺序，输出任意一种均可。

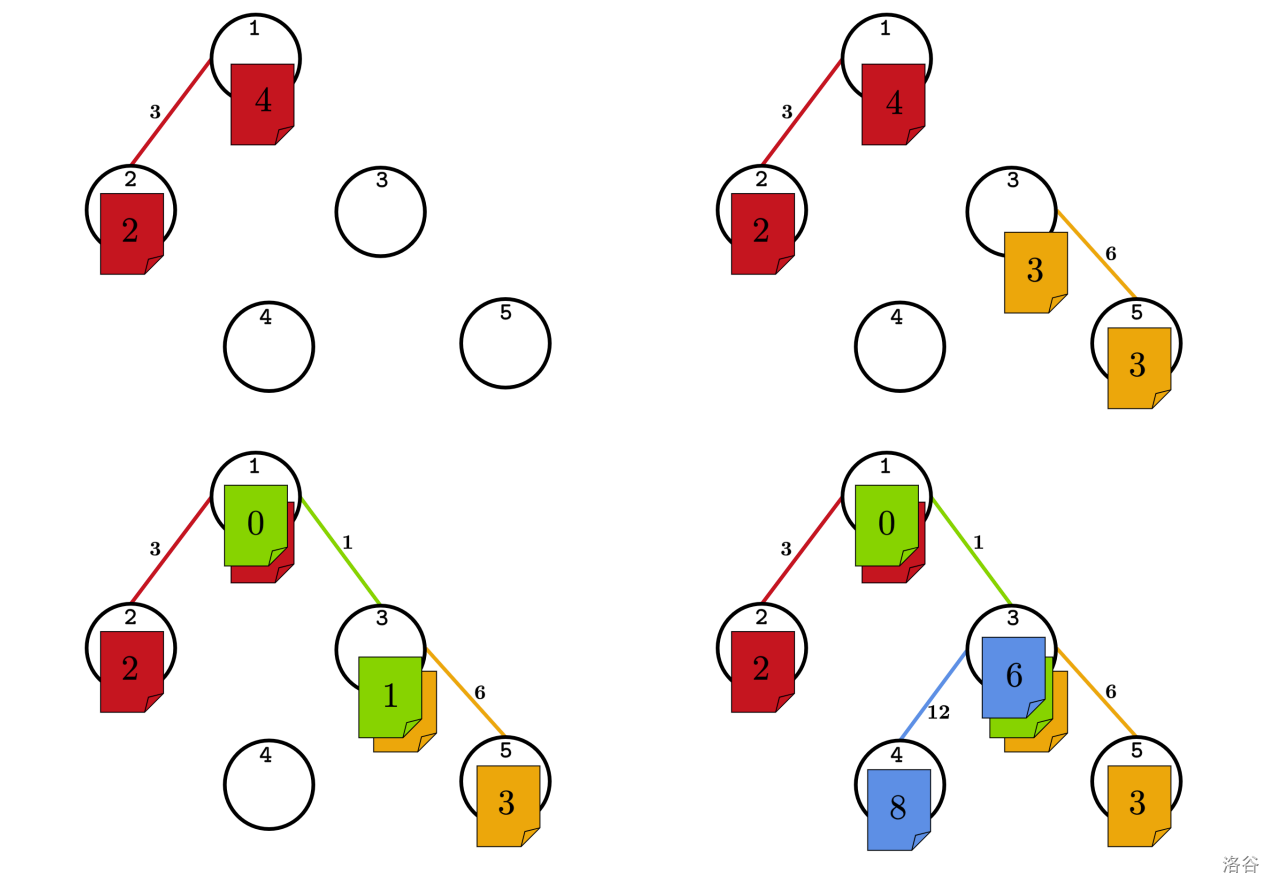
### 说明 在第一个样例中，可能的顺序之一为 $[1, 4, 2, 3]$。按时间顺序，第 $1$ 条联系连接了 $A=1$ 和 $B=2$，$c_A=4, c_B=2, w_{AB}=3$，$3 \leq 2+4$，证据合理。第 $2$ 条联系连接了 $A=3$ 和 $B=5$，$c_A=3, c_B=3, w_{AB}=6$，$6 \leq 3+3$，证据合理。第 $3$ 条联系连接了 $A=1$ 和 $B=3$，$c_A=0, c_B=1, w_{AB}=1$，$1 \leq 0+1$，证据合理。第 $4$ 条联系连接了 $A=3$ 和 $B=4$，$c_A=6, c_B=8, w_{AB}=12$，$12 \leq 6+8$，证据合理。参见下图更易理解。 :::align{center}  ::: ### 计分方式 本题共九组测试。只有通过该组及其所有依赖组全部测试，才能获得该组分数。请注意，部分组无需通过样例测试。**Offline-evaluation** 表示该组的结果仅在比赛结束后可见。 | 组别 | 分值 | 额外约束 | < | 依赖组 | 备注 | |:-----:|:------:|:----------------------:|:--:|:---------------:|:-------:| | | | $n$ | $a_i, b_i, c_i, w_i$ | | | | 0 | 0 | -- | -- | -- | 样例。 | | 1 | 10 | $n \le 10$ | -- | 0 | -- | | 2 | 15 | -- | $a_i = i, b_i = i+1$ 对所有 $i$ | -- | -- | | 3 | 8 | -- | $a_i = 1, b_i = i+1$ 对所有 $i$ | -- | -- | | 4 | 9 | -- | $a_i \leq 2, b_i = i+1$ 对所有 $i$ | 3 | -- | | 5 | 7 | $n \le 1000$ | $c_{i,1} \leq c_{i,2} \leq \ldots \leq c_{i, deg_i}$ 对所有 $i$ | -- | -- | | 6 | 7 | $n \le 1000$ | $c_{i, j} = 0$ 对所有 $1 \le i \le n$ 且 $j \geq 2$ | -- | -- | | 7 | 17 | -- | $\displaystyle\sum_{v=1}^{n} \displaystyle\sum_{i=1}^{deg_v} c_{v,i} = \displaystyle\sum_{i=1}^{n-1} w_i$ | -- | -- | | 8 | 16 | $n \le 1000$ | -- | 0, 1, 5, 6 | -- | | 9 | 11 | -- | -- | 0 -- 8 | **Offline-evaluation** | 翻译由 ChatGPT-4.1 完成。