P13508 [OOI 2024] Burenka and Pether

曾几何时，Burlyandia 的公主 Burenka 决定让她的朋友 ReLu 开心一下。她知道 ReLu 也热衷于加密货币，于是 Burenka 决定创立属于自己的区块链加密货币，命名为 **Pether**。 在接受了一位个人成长与网络安全领域专家的课程培训后，Burenka 决定要让 **Pether** 拥有最强的安全保护。结果，由于极其复杂且曲折的限制，并非所有用户都可以互相转账 **Pether**。 **Pether** 区块链的结构确实复杂且曲折。所有用户编号为 $1$ 到 $n$。每个用户都分配有一个**唯一**的标识符 $a_i$。此外，货币系统还设定了一个安全参数 $d$。 用户 $i$ 只有在 $i < j$ 且 $a_i < a_j$ 时，才能直接给用户 $j$ 转账。但这还不够！用户之间的直接转账还需要经过若干中间用户组成的交易链。在每一步交易中，每个后续中间用户（包括最终的 $j$）的编号都必须递增，且每次编号增加不能超过 $d$。此外，除 $i$ 和 $j$ 之外的所有中间用户，其标识符必须**严格小于** $a_i$。 更正式地说，用户 $i$ 能否直接向用户 $j$ 转账，需要满足以下条件： - $i < j$ - $a_i < a_j$ - 存在一组长度为 $k$ 的中间用户序列 $x$，使得： - $i = x_1 < x_2 < \ldots < x_{k-1} < x_k = j$ - 对所有 $1 \le t \le k-1$，有 $x_{t+1} - x_t \le d$ - 对所有 $2 \le t \le k-1$，有 $a_{x_t} < a_i$ Burenka 现在请你这位熟悉编程的朋友，帮她理解这个系统，并判断一些用户对之间能否转账 **Pether**。 你需要回答 $q$ 个询问。每个询问给定一对用户，询问是否存在一条（可能经过中间用户的）直接转账路径，使得可以从 $u_i$ 转账到 $v_i$。部分询问还要求**最小化**转账次数（即最少经过多少次直接转账，从 $u_i$ 到 $v_i$）。注意，在每次直接转账的实现过程中，不要求最小化中间用户数。

第一行包含三个整数 $n$、$d$ 和 $g$，分别表示用户数、安全参数和测试组编号，$1 \leq n, d \leq 3\times10^5$，$0 \leq g \leq 12$。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$，表示每个用户的唯一标识符，$1 \leq a_i \leq n$，保证所有 $a_i$ 互不相同。 第三行一个整数 $q$，表示询问数量，$1 \leq q \leq 3\times10^5$。 接下来 $q$ 行，每行三个整数 $t_i, u_i, v_i$，$t_i \in \{1, 2\}$，$1 \leq u_i < v_i \leq n$。其中 $u_i$ 是付款用户，$v_i$ 是收款用户。若 $t_i = 1$，只需判断能否转账；若 $t_i = 2$，还需输出从 $u_i$ 到 $v_i$ 的最少直接转账次数。

输出 $q$ 行，第 $i$ 行为第 $i$ 个询问的答案。 若不能从 $u_i$ 转账到 $v_i$，输出 $0$。否则，若 $t_i = 1$，输出 $1$；若 $t_i = 2$，输出从 $u_i$ 到 $v_i$ 的最小直接转账次数。

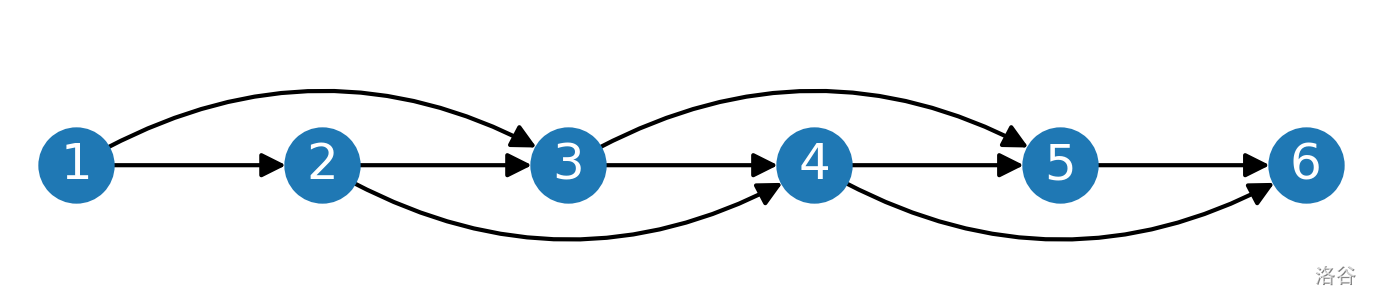
### 说明 在第一个样例中，用户之间的直接转账关系如下图：  第一个询问中，用户 $1$ 可通过用户 $2$ 作为中间人，经过 $2$ 次直接转账，将 **Pether** 转给用户 $3$。 第二个询问，用户 $1$ 无法直接转账给用户 $2$，因为 $a_1 = 2 > a_2 = 1$。 第三个询问，$1 \rightarrow 3 \rightarrow 4$，共 $2$ 次直接转账即可到达。因 $t_3 = 1$，只需判断可达性，输出 $1$。 第四个询问，可以 $1 \rightarrow 3 \rightarrow 4 \rightarrow 5$，共 $3$ 次直接转账。 第二个样例中，直接转账关系如下：  第三个样例中，直接转账关系如下：  ### 计分方式 本题共十二组测试。只有通过该组及其所有依赖组全部测试，才能获得该组分数。部分组不要求通过样例测试。**Offline-evaluation** 表示该组结果仅在赛后可见。 | 组别 | 分值 | $n$ | $q$ | 依赖组 | 特殊限制 | |:-----:|:----------------------:|:-:|:------:|:---------------:|:-------:| | 0 | 0 | $\le 3\times 10^5$ | $\le 3\times 10^5$ | 无 | 样例。 | | 1 | 10 | $\le 100$ | $\le 100$ | ^ | 无特殊限制。| | 2 | 7 | $\le 1000$ | $\le 3\times 10^5$ | $1$ | ^ | | 3 | 14 | $\le 3\times 10^5$ | ^ | 无 | $a_n = n, v_i = n$ | | 4 | 10 | ^ | $= 1$ | ^ |$v_i = n$ | | 5 | 9 | ^ | $\le 3\times 10^5$ | $3,4$ |^ | | 6 | 7 | ^ | ^ | 无 | $t_i=2$，答案不超过 $10$。 | | 7 | 7 | ^ | ^ | $1,6$ | $t_i=2$，答案不超过 $150$。 | | 8 | 13 | ^ | ^ | 无 | $t_i = 1$。 | | 9 | 10 | $\le 5\times10^4$ | $\le 5\times10^4$ | $1$ | 无特殊限制。 | | 10 | 4 | $\le 10^5$ | $\le 10^5$ | $1,9$ | ^ | | 11 | 4 | $\le 2\times10^5$ | $\le 2\times10^5$ | $1,9,10$ | ^ | | 12 | 5 | $\le 3\times 10^5$ | $\le 3\times 10^5$ | $0\sim11$ | **Offline-evaluation.** | 翻译由 ChatGPT-4.1 完成。