P13511 [KOI 2025 #1] 等腰直角三角形

试题来源：。中文翻译做了少量本土化修改。 按照[署名—非商业性使用—相同方式共享 4.0 协议国际版](https://creativecommons.org/licenses/by-nc-sa/4.0/deed.zh-hans)进行授权。

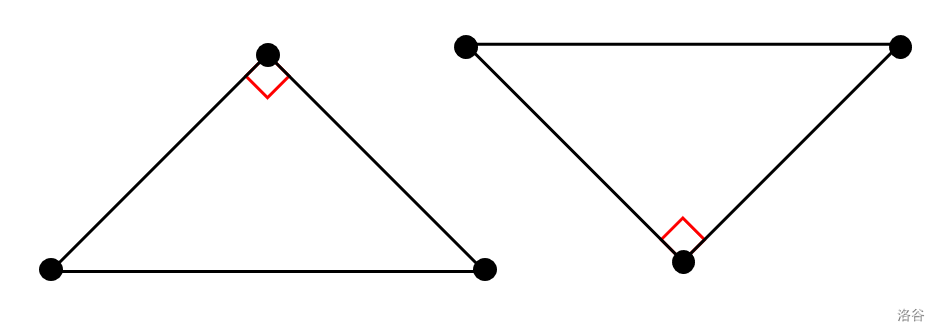
在二维平面上有 $N$ 个不同的点。对于每个 $1 \le i \le N$ 的 $i$，第 $i$ 个点的坐标为 $(x_i, y_i)$。 **等腰三角形**是指三条边中有两条边长度相等的三角形。**直角三角形**是指一个内角为直角 ($90^\circ$) 的三角形。直角三角形的**斜边**是指直角三角形中与直角相对的边，也是长度最长的边。**等腰直角三角形**是指既是直角三角形又是等腰三角形的三角形。即，三角形的一个内角为直角，且除斜边外的两条直角边长度相等的三角形。 请编写一个程序，找出满足以下两个条件的所有等腰直角三角形中，斜边长度最短的那个，并输出其斜边长度。 * $N$ 个点 $(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)$ 都位于等腰直角三角形的边界（边上）或其内部。如果某个点位于等腰直角三角形的顶点上，也视为位于边界上。 * 斜边与 $x$ 轴平行。也就是说，等腰直角三角形斜边的两个端点的 $y$ 坐标相同。这意味着只有如下图所示的两种等腰直角三角形满足条件：直角顶点在斜边上方的，和直角顶点在斜边下方的。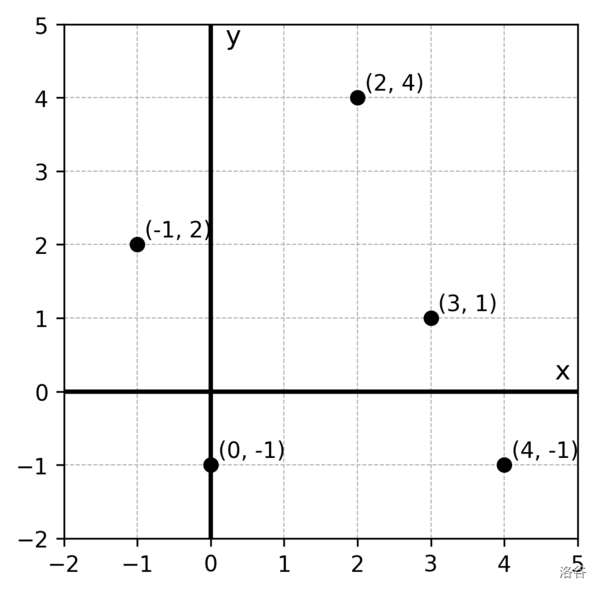  例如，假设给定如下图所示的 5 个点：$(0, -1), (2, 4), (4, -1), (-1, 2), (3, 1)$。点本身没有大小，但在图中为了方便观察，用圆形表示。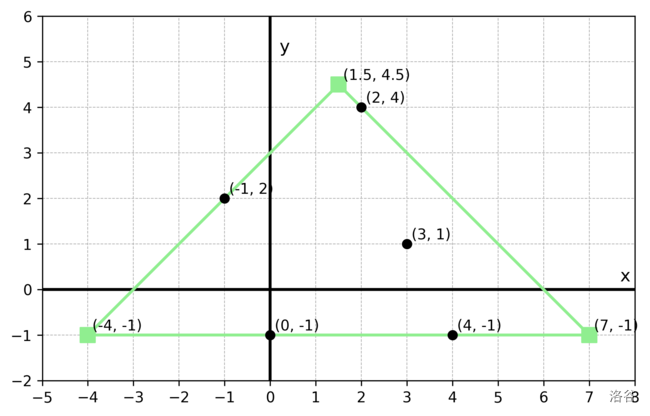  在直角顶点位于斜边上方的等腰直角三角形中，斜边最短的是如下图所示的，三个顶点为 $(1.5, 4.5), (-4, -1), (7, -1)$ 的三角形，这个等腰直角三角形的斜边长度为 11。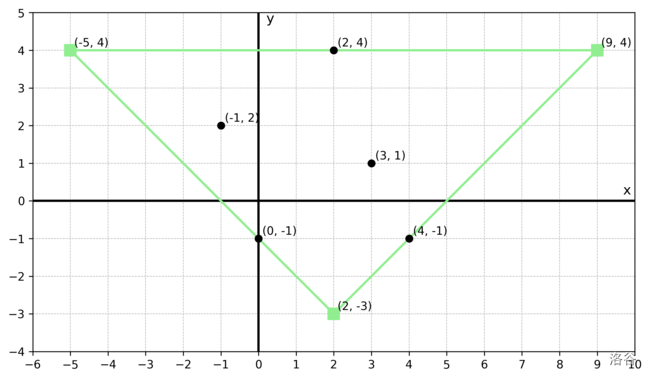  在直角顶点位于斜边下方的等腰直角三角形中，斜边最短的是如下图所示的，三个顶点为 $(2, -3), (-5, 4), (9, 4)$ 的三角形，这个等腰直角三角形的斜边长度为 14。  在这两种等腰直角三角形中，斜边较短的是直角顶点位于斜边上方的情况，因此所求的长度为 11。

第一行给定一个整数 $N$。 接下来的 $N$ 行中，第 $i$ ($1 \le i \le N$) 行给定两个整数 $x_i$ 和 $y_i$，以空格分隔。

在第一行输出满足所有条件的等腰直角三角形中，斜边长度最短的那个的斜边长度。可以证明答案总是一个整数。

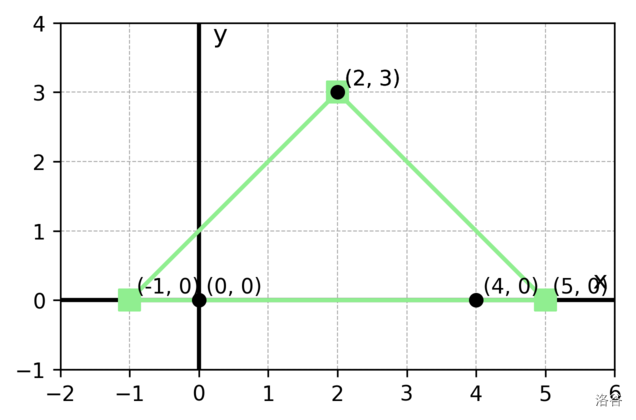
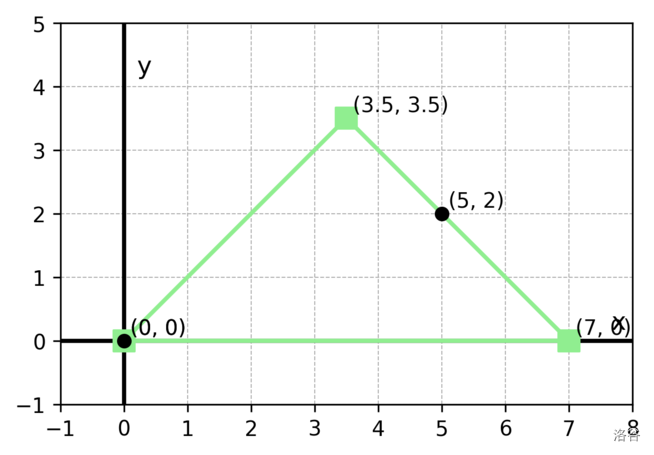
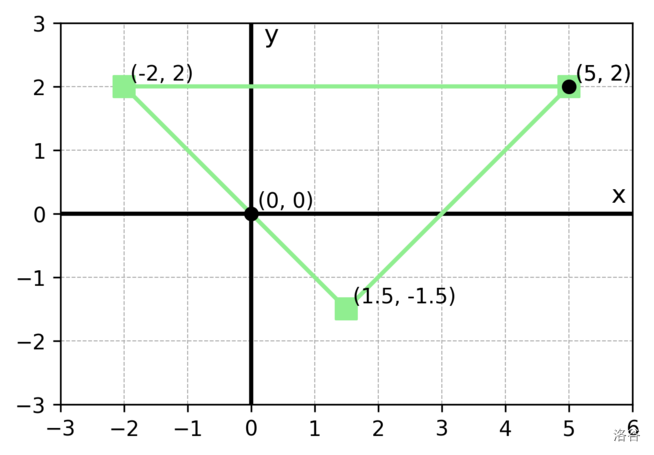
### 样例 1 解释 以 $(-1, 0), (2, 3), (5, 0)$ 为三个顶点的等腰直角三角形满足所有条件，其斜边长度为 6，是最短的。  ### 样例 2 解释 满足所有条件且斜边长度为 7 的等腰直角三角形有如下两种。 * 以 $(0, 0), (7, 0), (3.5, 3.5)$ 为三个顶点的三角形  * 以 $(-2, 2), (5, 2), (1.5, -1.5)$ 为三个顶点的三角形  ### 限制条件 * 给定的所有数都是整数。 * $2 \le N \le 100,000$。 * 对于每个 $1 \le i \le N$ 的 $i$，有 $-100,000,000 \le x_i, y_i \le 100,000,000$。 * 给定的 $N$ 个点都各不相同。也就是说，对于所有 $1 \le i < j \le N$ 的 $i, j$，都有 $x_i \ne x_j$ 或 $y_i \ne y_j$。 ### 子任务 1. (10 分) $N \le 2$。 2. (18 分) $N \le 3$。 3. (20 分) $N \le 50$，且对于每个 $1 \le i \le N$ 的 $i$，有 $-30 \le x_i, y_i \le 30$。 4. (10 分) $N \le 50$。 5. (4 分) 对于每个 $2 \le i \le N$ 的 $i$，有 $y_i = y_{i-1}$。也就是说，所有点的 $y$ 坐标都相同。 6. (6 分) 对于每个 $1 \le i \le N$ 的 $i$，有 $x_i = y_i$。 7. (10 分) 在所有满足给定条件且斜边长度最短的等腰直角三角形中，至少有一个的斜边中点是 $(0, 0)$。 8. (22 分) 无附加限制条件。