P13537 [IOI 2025] World Map

Mr. Pacha, a Bolivian archeologist, discovered an ancient document near Tiwanaku that describes the world during the Tiwanaku Period (300-1000 CE). At that time, there were $N$ countries, numbered from 1 to $N$. In the document, there is a list of $M$ different pairs of adjacent countries: $$\begin{aligned}(A[0], B[0]), (A[1], B[1]), \ldots, (A[M - 1], B[M - 1]).\end{aligned}$$ For each $i$ ($0 \leq i < M$), the document states that country $A[i]$ was adjacent to country $B[i]$ and vice versa. Pairs of countries not listed were not adjacent. Mr. Pacha wants to create a map of the world such that all adjacencies between countries are exactly as they were during the Tiwanaku Period. For this purpose, he first chooses a positive integer $K$. Then, he draws the map as a grid of $K \times K$ square cells, with rows numbered from 0 to $K - 1$ (top to bottom) and columns numbered from 0 to $K - 1$ (left to right). He wants to color each cell of the map using one of $N$ colors. The colors are numbered from 1 to $N$, and country $j$ ($1 \leq j \leq N$) is represented by color $j$. The coloring must satisfy all of the following **conditions**: - For each $j$ ($1 \leq j \leq N$), there is at least one cell with color $j$. - For each pair of adjacent countries $(A[i], B[i])$, there is at least one pair of adjacent cells such that one of them is colored $A[i]$ and the other is colored $B[i]$. Two cells are adjacent if they share a side. - For each pair of adjacent cells with different colors, the countries represented by these two colors were adjacent during the Tiwanaku Period. 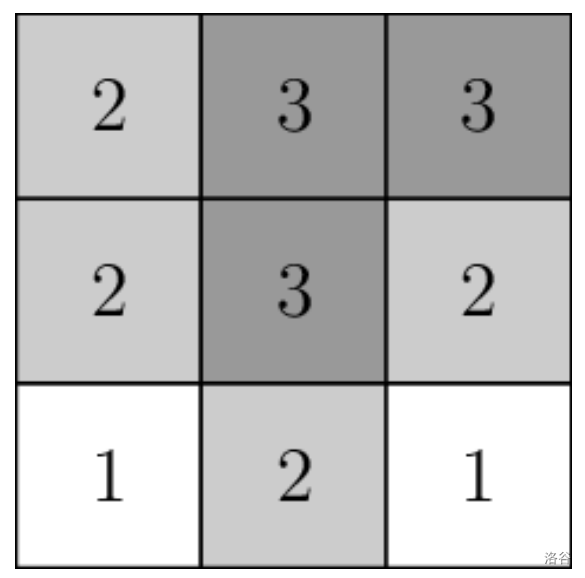For example, if $N = 3$, $M = 2$ and the pairs of adjacent countries are $(1, 2)$ and $(2, 3)$, then the pair $(1, 3)$ was not adjacent, and the following map of dimension $K = 3$ satisfies all the conditions. :::align{center}  ::: In particular, a country does **not** need to form a connected region on the map. In the map above, country 3 forms a connected region, while countries 1 and 2 form disconnected regions. Your task is to help Mr. Pacha choose a value of $K$ and create a map. The document guarantees that such a map exists. Since Mr. Pacha prefers smaller maps, in the last subtask your score depends on the value of $K$, and lower values of $K$ may result in a better score. However, finding the minimum possible value of $K$ is not required. ### Implementation Details You should implement the following procedure: ```cpp std::vector create_map(int N, int M, std::vector A, std::vector

The first line of the input should contain a single integer $T$, the number of scenarios. A description of $T$ scenarios should follow, each in the format specified below. ``` N M A[0] B[0] : A[M-1] B[M-1] ```

``` P Q[0] Q[1] ... Q[P-1] C[0][0] ... C[0][Q[0]-1] : C[P-1][0] ... C[P-1][Q[P-1]-1] ``` Here, $P$ is the length of the array $C$ returned by create_map, and $Q[i]$ ($0 \leq i < P$) is the length of $C[i]$. Note that line 3 in the output format is intentionally left blank.

### Example 1 Consider the following call: ``` create_map(3, 2, [1, 2], [2, 3]) ``` This is the example from the task description, so the procedure can return the following map. ``` [ [2, 3, 3], [2, 3, 2], [1, 2, 1] ] ``` ### Example 2 Consider the following call: ``` create_map(4, 4, [1, 1, 2, 3], [2, 3, 4, 4]) ``` In this example, $N = 4$, $M = 4$ and the country pairs $(1, 2)$, $(1, 3)$, $(2, 4)$, and $(3, 4)$ are adjacent. Consequently, the pairs $(1, 4)$ and $(2, 3)$ are not adjacent. The procedure can return the following map of dimension $K = 7$, which satisfies all the conditions. ``` [ [2, 1, 3, 3, 4, 3, 4], [2, 1, 3, 3, 3, 3, 3], [2, 1, 1, 1, 3, 4, 4], [2, 2, 2, 1, 3, 4, 3], [1, 1, 1, 2, 4, 4, 4], [2, 2, 1, 2, 2, 4, 3], [2, 2, 1, 2, 2, 4, 4] ] ``` The map could be smaller; for example, the procedure can return the following map of dimension $K = 2$. ``` [ [3, 1], [4, 2] ] ``` Note that both maps satisfy $K / N \leq 2$. ### Constraints * $1 \leq N \leq 40$ * $0 \leq M \leq \frac{N \cdot (N-1)}{2}$ * $1 \leq A[i] < B[i] \leq N$ for each $i$ such that $0 \leq i < M$. * The pairs $(A[0], B[0]), \ldots, (A[M-1], B[M-1])$ are distinct. * There exists at least one map which satisfies all the conditions. ### Subtasks and Scoring | Subtask | Score | Additional Constraints | | :-: | :-: | :-: | | 1 | 5 | $M = N - 1$, $A[i] = i + 1$, $B[i] = i + 2$ for each $0 \leq i < M$. | | 2 | 10 | $M = N - 1$ | | 3 | 7 | $M = \frac{N \cdot (N - 1)}{2}$ | | 4 | 8 | Country 1 is adjacent to all other countries. Some other pairs of countries may also be adjacent. | | 5 | 14 | $N \leq 15$ | | 6 | 56 | No additional constraints. | In subtask 6, your score depends on the value of $K$. - If any map returned by create_map does not satisfy all the conditions, your score for the subtask will be $0$. - Otherwise, let $R$ be the **maximum** value of $K/N$ over all calls to `create_map`. Then, you receive a **partial score** according to the following table: | Limits | Score | | :-: | :-: | | $6 < R$ | $0$ | | $4 < R \leq 6$ | $14$ | | $3 < R \leq 4$ | $28$ | | $2.5 < R \leq 3$ | $42$ | | $2 < R \leq 2.5$ | $49$ | | $R \leq 2$ | $56$ |