P13540 [IOI 2025] Obstacles for a Llama
Description
A llama wants to travel through the Andean Plateau. It has a map of the plateau in the form of a grid of $N \times M$ square cells. The rows of the map are numbered from $0$ to $N-1$ from top to bottom, and the columns are numbered from $0$ to $M-1$ from left to right. The cell of the map in row $i$ and column $j$ ($0 \leq i < N$, $0 \leq j < M$) is denoted by $(i, j)$.
The llama has studied the climate of the plateau and discovered that all cells in each row of the map have the same **temperature** and all cells in each column of the map have the same **humidity**. The llama has given you two integer arrays $T$ and $H$ of length $N$ and $M$ respectively. Here $T[i]$ ($0 \leq i < N$) indicates the temperature of the cells in row $i$, and $H[j]$ ($0 \leq j < M$) indicates the humidity of the cells in column $j$.
The llama has also studied the flora of the plateau and noticed that a cell $(i, j)$ is **free of vegetation** if and only if its temperature is greater than its humidity, formally $T[i] > H[j]$.
The llama can travel across the plateau only by following **valid paths**. A valid path is a sequence of distinct cells that satisfy the following conditions:
- Each pair of consecutive cells in the path shares a common side.
- All cells in the path are free of vegetation.
Your task is to answer $Q$ questions. For each question, you are given four integers: $L$, $R$, $S$, and $D$. You must determine whether there exists a valid path such that:
- The path starts at cell $(0, S)$ and ends at cell $(0, D)$.
- All cells in the path lie within columns $L$ to $R$, inclusive.
It is guaranteed that both $(0, S)$ and $(0, D)$ are free of vegetation.
### Implementation Details
The first procedure you should implement is:
```cpp
void initialize(std::vector T, std::vector H)
```
- $T$: an array of length $N$ specifying the temperature in each row.
- $H$: an array of length $M$ specifying the humidity in each column.
- This procedure is called exactly once for each test case, before any calls to `can_reach`.
The second procedure you should implement is:
```cpp
bool can_reach(int L, int R, int S, int D)
```
- $L, R, S, D$: integers describing a question.
- This procedure is called $Q$ times for each test case.
This procedure should return `true` if and only if there exists a valid path from cell $(0, S)$ to cell $(0, D)$, such that all cells in the path lie within columns $L$ to $R$, inclusive.
Input Format
Input format:
```
N M
T[0] T[1] ... T[N-1]
H[0] H[1] ... H[M-1]
Q
L[0] R[0] S[0] D[0]
L[1] R[1] S[1] D[1]
...
L[Q-1] R[Q-1] S[Q-1] D[Q-1]
```
Here, $L[k]$, $R[k]$, $S[k]$ and $D[k]$ ($0 \leq k < Q$) specify the parameters for each call to `can_reach`.
Output Format
Output format:
```
A[0]
A[1]
...
A[Q-1]
```
Here, $A[k]$ ($0 \leq k < Q$) is $1$ if the call `can_reach(L[k], R[k], S[k], D[k])` returned true, and $0$ otherwise.
Explanation/Hint
### Example
Consider the following call:
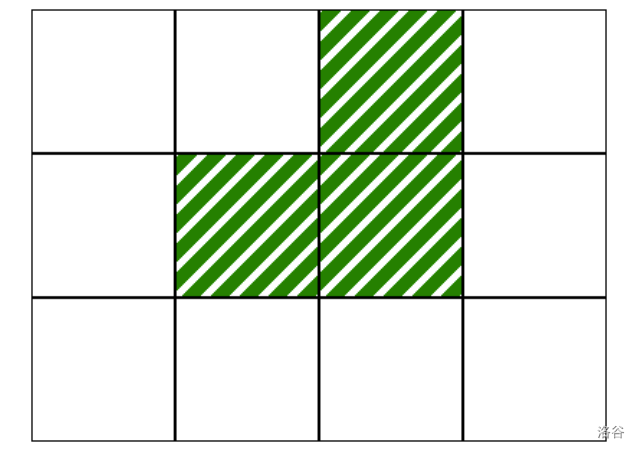
```cpp
initialize([2, 1, 3], [0, 1, 2, 0])
```
This corresponds to the map in the following image, where white cells are free of vegetation:
As the first question, consider the following call:
```
can_reach(0, 3, 1, 3)
```
This corresponds to the scenario in the following image, where the thick vertical lines indicate the range of columns from $L = 0$ to $R = 3$, and the black disks indicate the starting and ending cells:
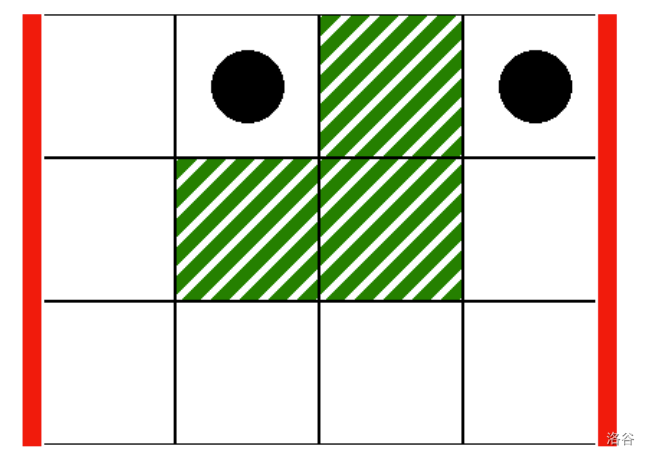
In this case, the llama can reach from cell $(0, 1)$ to cell $(0, 3)$ through the following valid path:
$$(0, 1), (0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (2, 3), (1, 3), (0, 3)$$
Therefore, this call should return true.
As the second question, consider the following call:
```
can_reach(1, 3, 1, 3)
```
This corresponds to the scenario in the following image:
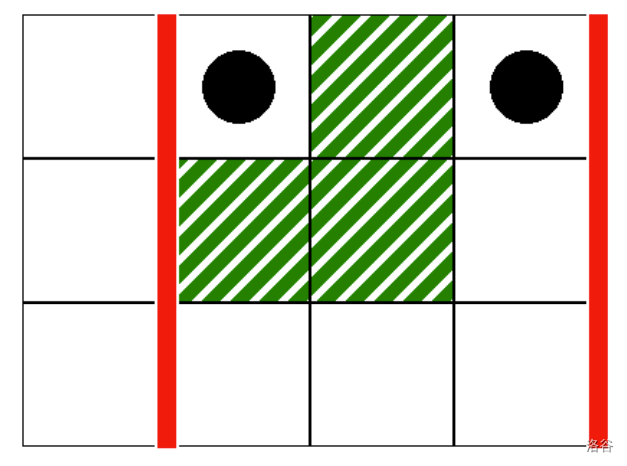
In this case, there is no valid path from cell $(0,1)$ to cell $(0,3)$, such that all cells in the path lie within columns $1$ to $3$, inclusive. Therefore, this call should return false.
### Constraints
- $1 \leq N, M, Q \leq 200000$
- $0 \leq T[i] \leq 10^9$ for each $i$ such that $0 \leq i < N$.
- $0 \leq H[j] \leq 10^9$ for each $j$ such that $0 \leq j < M$.
- $0 \leq L \leq R < M$
- $L \leq S \leq R$
- $L \leq D \leq R$
- Both cells $(0, S)$ and $(0, D)$ are free of vegetation.
### Subtasks
| Subtask | Score | Additional Constraints |
| :-: | :-: | :-: |
| 1 | 10 | $L = 0, R = M - 1$ for each question. $N = 1$. |
| 2 | 14 | $L = 0, R = M - 1$ for each question. $T[i - 1] \leq T[i]$ for each $i$ such that $1 \leq i < N$. |
| 3 | 13 | $L = 0, R = M - 1$ for each question. $N = 3$ and $T = [2, 1, 3]$. |
| 4 | 21 | $L = 0, R = M - 1$ for each question. $Q \leq 10$. |
| 5 | 25 | $L = 0, R = M - 1$ for each question. |
| 6 | 17 | No additional constraints. |