P13540 [IOI 2025] 羊驼的坎坷之旅(obstacles)
题目描述
一只羊驼想要穿越安第斯高原。它有一张高原的地图,为 $N \times M$ 个方形单元格组成的网格。地图的行从上到下以 $0$ 到 $N-1$ 编号,列从左到右以 $0$ 到 $M-1$ 编号。地图中第 $i$ 行第 $j$ 列的单元格($0 \leq i < N$,$0 \leq j < M$)记为 $(i, j)$。
这只羊驼研究了高原的气候,发现地图中每行的所有单元格具有相同的**温度**(temperature),每列的所有单元格具有相同的**湿度**(humidity)。它给了你两个长度分别为 $N$ 和 $M$ 的整数数组 $T$ 和 $H$。这里,$T[i]$($0 \leq i < N$)表示第 $i$ 行所有单元格的温度,$H[j]$($0 \leq j < M$)表示第 $j$ 列所有单元格的湿度。
羊驼还研究了高原的植被情况,注意到一个单元格 $(i, j)$ **无植被**的充要条件是其温度大于湿度,形式化为 $T[i] > H[j]$。
羊驼只能通过**合法路径**在高原上移动。合法路径定义为满足以下条件的单元格序列:
* 路径中每对连续单元格之间共享一条边。
* 路径中所有单元格均为无植被的单元格。
你的任务是回答 $Q$ 次询问。对于每次询问,你将获得四个整数:$L$,$R$,$S$ 和 $D$。你需要判断是否存在一条合法路径,使得:
* 路径起点是单元格 $(0, S)$,终点是单元格 $(0, D)$。
* 路径中的所有单元格位于列 $L$ 到 $R$ 之间。
保证 $(0, S)$ 和 $(0, D)$ 均为无植被的单元格。
### 实现细节
你需要实现的第一个函数为:
```
void initialize(std::vector T, std::vector H)
```
* $T$:长度为 $N$ 的数组,表示每行的温度。
* $H$:长度为 $M$ 的数组,表示每列的湿度。
* 对每个测试用例,该函数恰好被调用一次。该函数在 `can_reach` 之前调用。
你需要实现的第二个函数为:
```
bool can_reach(int L, int R, int S, int D)
```
* $L, R, S, D$:描述询问的四个整数。
* 对每个测试用例,该函数会被调用 $Q$ 次。
当且仅当存在一条从单元格 $(0, S)$ 到单元格 $(0, D)$ 的合法路径,使得路径中的所有单元格位于列 $L$ 到 $R$ 之间时,该函数返回 `true`。
输入格式
输入格式:
```
N M
T[0] T[1] ... T[N-1]
H[0] H[1] ... H[M-1]
Q
L[0] R[0] S[0] D[0]
L[1] R[1] S[1] D[1]
...
L[Q-1] R[Q-1] S[Q-1] D[Q-1]
```
其中,$L[k], R[k], S[k]$ 和 $D[k]$ ($0 \leq k < Q$) 指定了每次调用 `can_reach` 的参数。
输出格式
输出格式:
```
A[0]
A[1]
...
A[Q-1]
```
其中, 当函数调用 `can_reach(L[k], R[k], S[k], D[k])` 的返回值为 `true` 时, $A[k]$ ($0 \leq k < Q$)为 $1$, 否则为 $0$。
说明/提示
### 例子
考虑以下调用。
```
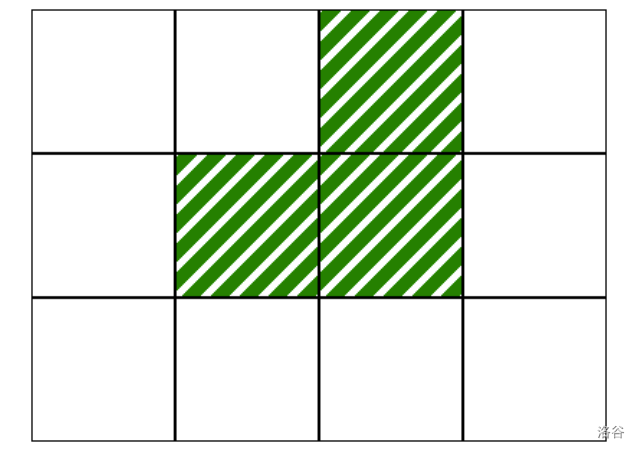
initialize([2, 1, 3], [0, 1, 2, 0])
```
这对应于如下地图,其中白色单元格无植被:
对第一次询问,考虑以下调用:
```
can_reach(0, 3, 1, 3)
```
这对应如下场景,其中竖直粗线表示列范围 $L = 0$ 到 $R = 3$,黑色圆点表示起点和终点:
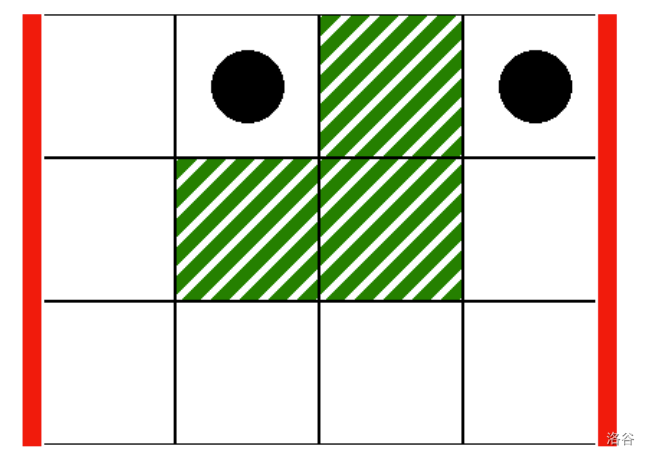
在这种情况下,羊驼可以通过以下合法路径从单元格 $(0,1)$ 移动到 $(0,3)$:
$$(0,1), (0,0), (1,0), (2,0), (2,1), (2,2), (2,3), (1,3), (0,3)$$
因此,该调用应返回 `true`。
对第二次询问,考虑以下调用:
```
can_reach(1, 3, 1, 3)
```
其对应如下场景:
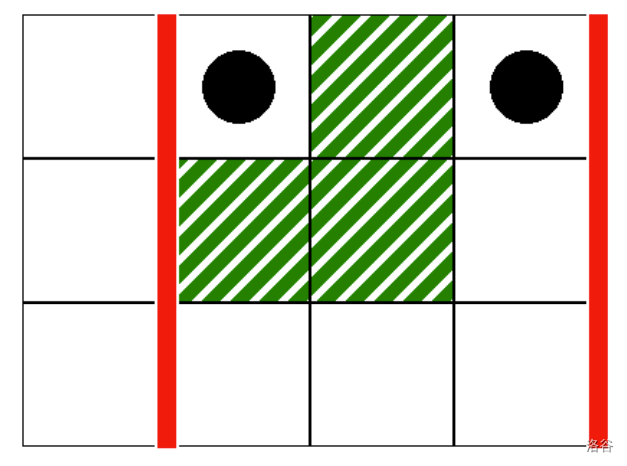
在这种情况下,不存在从单元格 $(0, 1)$ 到 $(0, 3)$ 的合法路径,使得路径中的所有单元格位于列 $1$ 到 $3$ 之间。因此,该调用应返回 `false`。
### 约束条件
* $1 \leq N, M, Q \leq 200\,000$
* 对每个满足 $0 \leq i < N$ 的 $i$,都有 $0 \leq T[i] \leq 10^9$。
* 对每个满足 $0 \leq i < M$ 的 $j$,都有 $0 \leq H[j] \leq 10^9$。
* $0 \leq L \leq R < M$
* $L \leq S \leq R$
* $L \leq D \leq R$
* $(0, S)$ 和 $(0, D)$ 均为无植被的单元格。
### 子任务
| 子任务 | 分数 | 额外的约束条件 |
| :-----: | :----: | ---------------------- |
| 1 | $10$ | 对每次询问,都有 $L = 0$, $R = M - 1$。$N = 1$。 |
| 2 | $14$ | 对每次询问,都有 $L = 0$, $R = M - 1$。对每个满足 $1 \leq i < N$ 的 $i$,都有$T[i-1] \leq T[i]$。 |
| 3 | $13$ | 对每次询问,都有 $L = 0$, $R = M - 1$。$N = 3$ 和 $T = [2, 1, 3]$。 |
| 4 | $21$ | 对每次询问,都有 $L = 0$, $R = M - 1$。$Q \leq 10$。 |
| 5 | $25$ | 对每次询问,都有 $L = 0$, $R = M - 1$。|
| 6 | $17$ | 没有额外的约束条件。 |