P13564 「CZOI-R5」奶龙

[❤点击链接直达奶龙❤](/user/621382)。

现有一张 $n$ 个点，初始没有任何边的编号 $1\sim n$ 的图，给定长度为 $m$ 的数组 $A_i$，表示编号为 $A_i$ 的点上有一只奶龙，在每一次行动中，奶龙会沿着当前点连向其它点的边走向下一个点。 请你构造一张图，给定正整数 $k$，使得其满足： - 每个点的出度均为 $1$，不得有自环。 - 经过恰好 $k$ 次行动时，所有点都被至少一只奶龙经过，且在经过恰好 $k-1$ 次行动时，至少有一个点未被任何奶龙经过。 若无解则输出 `-1`。

第一行共三个整数，表示 $n,m,k$。 第二行共 $m$ 个正整数，其中第 $i$ 个数表示 $A_i$。

共 $n$ 行，每行输出两个正整数 $u,v$，表示有一条 $u\to v$ 的有向边。 本题使用 Special Judge，若有多种答案任意输出一种即可。

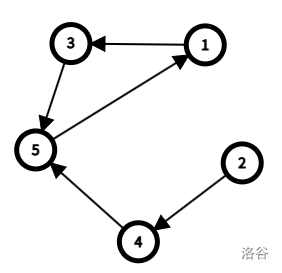
### 样例解释 对于样例组 #1 中的构造方案，图形态如下。  初始点 $1,2$ 上分别有一只奶龙，走第一轮后可以到达 $3,4$，走第二轮后可以到达 $5$，符合题意。 ### 数据范围 |子任务编号|$n$|$m$|$k$|分值| |:-:|:-:|:-:|:-:|:-:| |$1$|$\le 8$|$\le 8$|$< 8$|$10$| |$2$|$\le 2\times 10^5$|$=1$|$< 2\times 10^5$|$15$| |$3$|$\le 2\times 10^5$|$\le 2\times 10^5$|$=1$|$15$| |$4$|$\le 2\times 10^5$|$\le 2\times 10^5$|$< 2\times 10^5$|$60$| 对于 $100\%$ 的数据，保证 $1\le m\le n\le 2\times 10^5$，$1\le k< n$，$1\le A_i\le n$，$A_i$ 互不相同。另外，为便于编写 Special Judge 保证 $1\le m\times k \le 10^6$，不保证与你的解题过程是否有关。