P13566 「CZOI-R5」青蛙的旅行

小 L 是一只青蛙，他现在准备在 A 城旅行。

A 城是一个 $n\times m$ 的矩阵。有一个给定的数 $k$。还有一个变量 $w$，初始为 $0$。记 $(r,c)$ 表示第 $r$ 行第 $c$ 列。 这个矩阵中有 $t$ 个特殊点，第 $i$ 个在 $(x_i,y_i)$，类型为 $p_i$（$p_i\in\{1,2\}$），若 $p_i=2$，则有一个额外属性 $s_i$。**保证不存在 $i,j$ 满足 $i\neq j$ 且 $x_i=x_j,y_i=y_j$。** 小 L 初始在 $(1,1)$，它可以做任意次以下跳跃方法之一**直到它到达** $(n,m)$。假设它现在在 $(a,b)$： - 选择一个 $h$，满足 $0\le h\le k$，且不存在 $1\le i\le h$ 使得 $(a+i,b)$ 为类型为 $2$ 的特殊点。接着跳到 $(a+h+1,b)$。 - 选择一个 $h$，满足 $0\le h\le k$，且不存在 $1\le i\le h$ 使得 $(a,b+i)$ 为类型为 $2$ 的特殊点。接着跳到 $(a,b+h+1)$。 - 选择一个 $h$，满足 $0\le h\le k$，且不存在 $1\le i\le h$ 使得 $(a+i,b+i)$ 为类型为 $2$ 的特殊点。接着跳到 $(a+h+1,b+h+1)$。 在每次跳跃后，假设跳到了 $(X,Y)$，若 $(X,Y)$ 是第 $Z$ 个特殊点，那么： - 若 $p_Z=1$，则 $w\leftarrow w+1$。 - 若 $p_Z=2$，令 $w\leftarrow w-s_Z$。 若某个方案中间某个时刻 $w

第一行输入 $4$ 个整数 $n,m,k,t$。 接下来 $t$ 行，每行先输入 $1$ 个整数 $p_i$，然后： - 若 $p_i=1$，则输入 $2$ 个整数 $x_i,y_i$，表示一个类型为 $1$ 的特殊点。 - 若 $p_i=2$，则输入 $3$ 个整数 $x_i,y_i,s_i$，表示一个类型为 $2$ 的特殊点。

第一行输出 $1$ 个整数，表示答案。

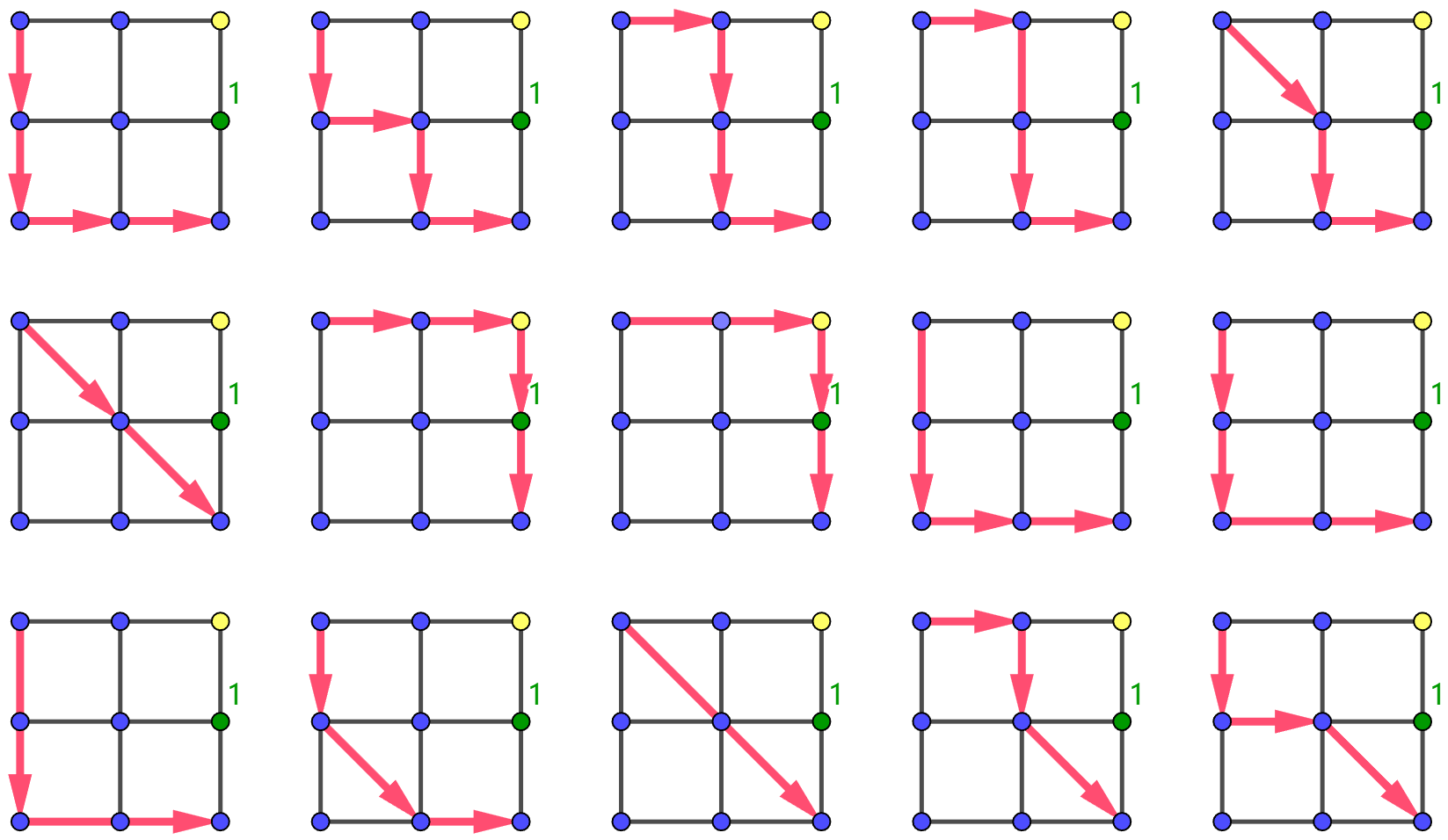
**【样例解释 #1】** 注：下列每个点代表一个格子；红色箭头为一次跳跃，箭头尾端为 $(X,Y)$；黄色点为 $p_i=1$ 的特殊点；绿色点为 $p_i=2$ 的特殊点。 以下 $15$ 种方案是合法的：  以下 $5$ 种方案不合法，因为在这些方案中，小 L 到 $(2,3)$ 后 $w=-1