P13567 「CZOI-R5」折跃点

宇宙中爆发了星际战争。

为了在星际战争中进行瞬间移动，我方已经在占领的星域中建立了 $n$ 个折跃点。所有折跃点构成一棵以折跃点 $1$ 为根的有根树。第 $i$ 个折跃点的能量值为 $a_i$。 我们称折跃点 $u$ 经过 $x$ 次连续折跃能到达折跃点 $v$，当且仅当从折跃点 $u$ 出发，走过 $x$ 条边后能到达折跃点 $v$，且过程中与折跃点 $1$ 的距离不断增加或不断减少。 现在要进行 $m$ 次以下维护操作： 1. **空间能量增强**：对于所有从折跃点 $u$ 经过 $x$ 次连续折跃能到达的折跃点，将其能量值加 $y$。 2. **折跃测试**：求所有从折跃点 $u$ 经过 $x$ 次连续折跃能到达的折跃点，能量值的和。

第一行输入 $2$ 个整数 $n, m$。 第二行输入 $n$ 个整数，第 $i$ 个为 $a_i$。 接下来 $n - 1$ 行，每行输入 $2$ 个整数 $u, v$，表示一条边。 接下来 $m$ 行，每行先输入 $1$ 个整数 $p$，然后： - 若 $p=1$，则输入 $3$ 个整数 $u,x,y$，表示一次**空间能量增强**。 - 若 $p=2$，则输入 $2$ 个整数 $u,x$，表示一次**折跃测试**。

输出若干行整数，即为所有**折跃测试**的结果。

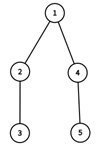
**【样例解释】**  这棵树如图。 第一次操作满足条件的折跃点为折跃点 $3,5$，操作后 $a=\{6,8,11,10,13\}$。 第二次操作满足条件的折跃点为折跃点 $1,5$，答案为 $6+13=19$。 第三次操作满足条件的折跃点为折跃点 $2$，答案为 $8$。 第四次操作满足条件的折跃点为折跃点 $1,3$，操作后 $a=\{10,8,15,10,13\}$。 第五次操作满足条件的折跃点为折跃点 $3,5$，答案为 $15+13=28$。 **【数据范围】** **本题采用捆绑测试**。 - Subtask #1（$15\text{ pts}$）：$n, m \le 10^3$。 - Subtask #2（$15\text{ pts}$）：$x \le 1$。 - Subtask #3（$25\text{ pts}$）：$x \le 50$。 - Subtask #4（$45\text{ pts}$）：无特殊限制。 对于 $100\%$ 的数据，$1\le u\le n\le3\times10^5$，$1 \le m \le 3 \times 10^5$，$1 \le a_i, y \le 10^9$，$0 \le x \le n$，$p\in\{1,2\}$。