P13588 [NWRRC 2023] H-Shaped Figures

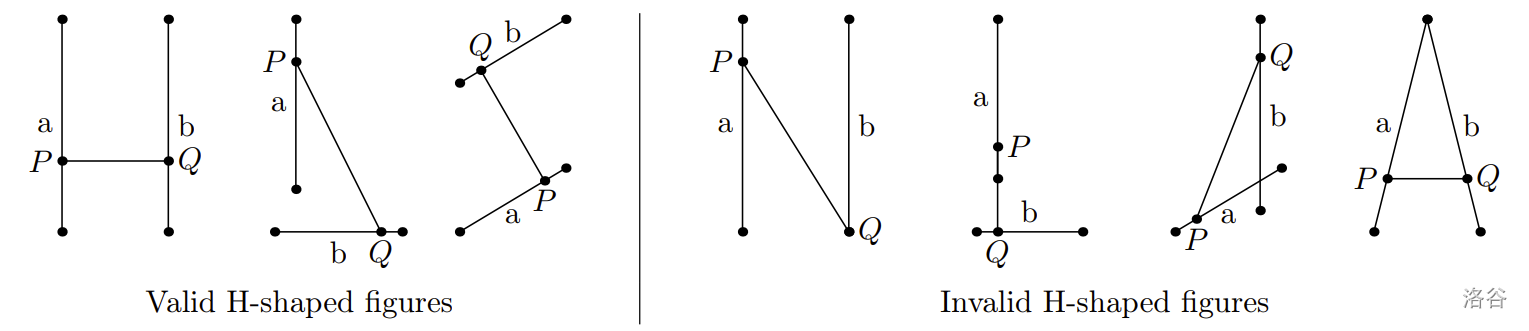
在去年的“K 形图形”问题取得巨大成功之后，今年我们带来了创新的“H 形图形”问题。我们还为接下来的 24 年做了一些计划。 设平面上的三条线段 $PQ$、$a$ 和 $b$ 构成一个 H 形图形，当且仅当： - 点 $P$ 严格在线段 $a$ 的内部，且线段 $PQ$ 与 $a$ 不共线； - 点 $Q$ 严格在线段 $b$ 的内部，且线段 $PQ$ 与 $b$ 不共线； - 线段 $a$ 和 $b$ 没有公共点。  给定点 $P$ 和 $Q$ 的坐标，以及 $n$ 条候选线段作为 $a$ 和 $b$。注意，给定的线段中可能有重合的，但它们仍应视为不同的线段。 请你计算有多少种方式可以选择一条线段作为 $a$，另一条线段作为 $b$，与给定的 $PQ$ 线段一起构成一个 H 形图形。

每个测试包含多组测试用例。第一行包含测试用例的数量 $t$（$1 \le t \le 10^5$）。接下来是每组测试用例的描述。 每组测试用例的第一行包含四个整数 $x_P, y_P, x_Q, y_Q$，表示点 $P$ 和 $Q$ 的坐标（$-10^9 \le x_P, y_P, x_Q, y_Q \le 10^9$）。保证 $P$ 和 $Q$ 不重合。 第二行包含一个整数 $n$，表示候选线段的数量（$2 \le n \le 2 \cdot 10^5$）。 接下来的 $n$ 行中，第 $i$ 行包含四个整数 $x_{i,1}, y_{i,1}, x_{i,2}, y_{i,2}$，表示第 $i$ 条线段的两个端点的坐标（$-10^9 \le x_{i,1}, y_{i,1}, x_{i,2}, y_{i,2} \le 10^9$）。所有线段长度均大于零。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每组测试用例，输出一个整数，表示使用给定的 $PQ$ 线段和两条候选线段构成 H 形图形的方案数。

由 ChatGPT 4.1 翻译